
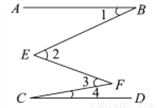
如图,已知∠1=250,∠2=450, ∠3=300,∠4=100.求证:AB//CD.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:解答题
如图所示,在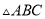 中,
中, 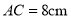 ,
, 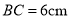 ,在
,在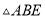 中,
中, 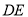 为
为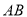 边上的高,
边上的高, 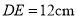 ,
, 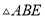 的面积
的面积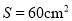 .
.
(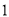 )求出
)求出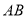 边的长.
边的长.
(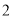 )你能求出
)你能求出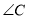 的度数吗?请试一试.
的度数吗?请试一试.

查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:单选题
如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )
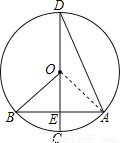
A. 3 B. 3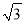 C.
C. 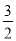 D.
D. 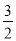
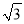
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
如图,在梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点O,若FO-EO=3,则BC-AD等于 ( )

A.4; B. 6; C. 8; D. 10.
B 【解析】 试题分析:AD∥BC且EF为梯形中位线,所以EF同样平分?BD,EO为△ABD中位线,OF为△DBC中位线。 ∴易知EO=AD,FO=BC。FO-EO=BC-AD=(BC-AD)=3,∴BC-AD=6查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
矩形具有而平行四边形不一定具有的性质是( )
A. 对角相等 B. 对边相等
C. 对角线相等 D. 对角线互相平分
C 【解析】试题解析:矩形的 对角线相等,而平行四边形的对角线不一定相等. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
已知:如图,∠1 =∠2,∠3 =∠4,∠5 =∠6.求证:ED∥FB.
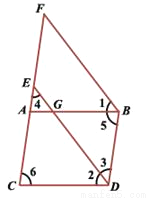
查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
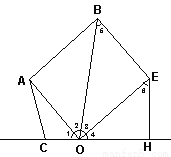
如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:填空题
点P(a﹣1,a2﹣9)在x轴负半轴上,则P点坐标是________.
(﹣4,0) 【解析】【解析】 由题意得:a2-9=0且a-1<0,解得:a=-3.故答案为:(-4,0).查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
下列各式中,在实数范围内能分解因式的是( )
A. x2+5 B. x2﹣5 C. x2+9 D. x2+x+1.
B 【解析】∵x 2 +5,x 2 +9,x 2 +x+1均是最简因式, ∴不能进行因式分解,故A、C、D错误; x 2 -5=(x+ )(x- ),故B正确, 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com