
一个不等边三角形的边长都是整数,且周长是12,这样的三角形共有多少个?
符合条件的三角形共有1个 【解析】试题分析:题设中已知数较少,只知道周长为12,应抓住不等边三角形的边长都是整数这一条件,依据三角形三边关系先确定出最大边的取值范围,则问题迎刃而解. 试题解析:设 a<b<c,则a+b+c>2c,即 2c<12,所以 c<6, 因为a,b,c 都是正整数,所以若c=3,则其他两边必然为a=1,b=2, 由于1+2=3,即 a+b=c,故线段... 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北师大版七年级数学下册达标检测 第三章 变量之间的关系 题型:单选题
某校组织学生到距学校6 km的光明科技馆参观.王红准备乘出租车去科技馆,出租车的收费标准如下表:
里程数 | 收费/元 |
3 km以下(含3 km) | 8.00 |
3 km以上每增加1 km | 1.80 |
则收费y(元)与出租车行驶里程数x(km)(x≥3)之间的关系式为( )
A. y=8x B. y=1.8x C. y=8+1.8x D. y=2.6+1.8x
D 【解析】∵3千米以上每增加1千米收费1.80元, ∴出租车行驶里程数x(x≥3)与收费y之间的关系式为: y=8+1.8(x-3)=1.8x+2.6. 故选:D.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第五章达标检测卷 题型:解答题
(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
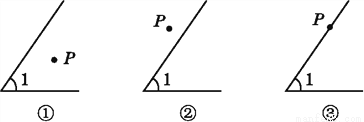
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
(1)作图见解析;(2)∠1+∠P=180°;(3).∠1=∠APB;∠1=∠APB或∠1+∠APB=180°(4)相等或互补 【解析】试题分析:(1)根据题目要求,结合题中条件,由点P分别向∠1的两边做垂线,即可得到∠P; (2)用量角器分别测量∠P与∠1的度数,即可得出二者的关系; (3)分别在其余两图中,按要求作出∠P,再测量,即可得到结论; (4)结合以上作图和结论...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:解答题
在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是多少?
120° 【解析】试题分析:需要分类讨论,C,D在AB同侧,∠AOC+∠COD+∠DOB=180°,易得∠BOD;C,D在AB异侧,∠COA+∠AOD=90°,∠AOD+∠BOD=180°,可得∠BOD. 试题解析: 【解析】 (1)如图,当OC,OD在AB一侧时, ∵OC⊥OD,∴∠COD=90°. ∵∠AOC=30°,∴∠BOD=180°-∠COD-∠AOC=6...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
已知在同一平面内:①两条直线相交成直角;②两条直线互相垂直;③一条直线是另一条直线的垂线.那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
D 【解析】垂直的定义:再同一平面内,两条直线相交成直角时,称这两条直线互相垂直,其中一条直线是另一条直线的垂线.由此可知三种因果关系都正确. 故选:D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册4.1.2认识三角形 同步练习 题型:填空题
科目:初中数学 来源:北师大版七年级数学下册同步要点3.2 用关系式表示的变量间关系 题型:解答题
某市出租车收费标准如下: 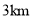 以内(含
以内(含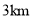 )收费
)收费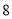 元;超过
元;超过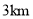 的部分每千米收费
的部分每千米收费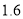 元.
元.
(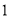 )写出应收费
)写出应收费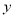 (元)与出租车行驶路程
(元)与出租车行驶路程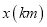 之间的关系式(其中
之间的关系式(其中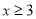 ).
).
(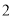 )小亮乘出租车行驶
)小亮乘出租车行驶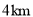 ,应付多少元?
,应付多少元?
(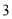 )小波付车费
)小波付车费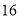 元,那么出租车行驶了多少千米?
元,那么出租车行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 单元测试卷 题型:解答题
如图,要设计一幅长为3xcm、宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度为acm,竖彩条的宽度为bcm,问空白区域的面积是多少?
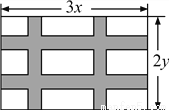
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:解答题
如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.
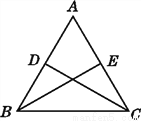
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com