
УќЬтЁАШ§НЧаЮЕФвЛИіЭтНЧЕШгкКЭЫќВЛЯрСкЕФСНИіФкНЧЕФКЭЁБЕФЬѕМўЪЧ________ЃЌНсТл________ЃЎ
вЛИіНЧЪЧШ§НЧаЮЕФЭтНЧ ЕШгкКЭЫќВЛЯрСкЕФСНИіФкНЧЕФКЭ ЁОНтЮіЁПЯШАбУќЬтаДГЩЁАШчЙћЁБЃЌЁАФЧУДЁБЕФаЮЪНЃЌЁАШчЙћЁБКѓУцЕФЪЧЬѕМўЃЌЁАФЧУДЁБКѓУцЕФЪЧНсТлЁЃУќЬтЁАШ§НЧаЮЕФвЛИіЭтНЧЕШгкКЭЫќВЛЯрСкЕФСНИіФкНЧЕФКЭЁБЕФЬѕМўЪЧвЛИіНЧЪЧШ§НЧаЮЕФЭтНЧЃЌНсТлЪЧЕШгкКЭЫќВЛЯрСкЕФСНИіФкНЧЕФКЭЃЎ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁЖЋВПЗжаЃ2017-2018бЇФъЦпФъМЖЩЯбЇЦкЦкФЉПМЪдЪ§бЇЪдОэ ЬтаЭЃКЕЅбЁЬт
ЙлВьЯТСаЕШЪНЃК
ЕквЛВу 1+2=3
ЕкЖўВу 4+5+6=7+8
ЕкШ§Ву 9+10+11+12=13+14+15
ЕкЫФВу 16+17+18+19+20=21+22+23+24
ЁЁ
дкЩЯЪіЕФЪ§зжБІЫўжаЃЌДгЩЯЭљЯТЪ§ЃЌ2018дкЕкЃЈ ЃЉВуЃЎ
A. 43 B. 44 C. 45 D. 46
B ЁОНтЮіЁПЁОНтЮіЁП ЕквЛВуЃКЕквЛИіЪ§ЮЊ12=1ЃЌзюКѓвЛИіЪ§ЮЊ22Љ1=3ЃЌЕкЖўВуЃКЕквЛИіЪ§ЮЊ22=4ЃЌзюКѓвЛИіЪ§ЮЊ32Љ1=8ЃЌЕкШ§ВуЃКЕквЛИіЪ§ЮЊ32=9ЃЌзюКѓвЛИіЪ§ЮЊ42Љ1=15ЃЌЁп442=1936ЃЌ452=2025ЃЌгжЁп1936ЃМ2018ЃМ2025ЃЌЁрдкЩЯЪіЪ§зжБІЫўжаЃЌДгЩЯЭљЯТЪ§ЃЌ2018дкЕк44ВуЃЌЙЪД№АИЮЊЃК44ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁЬЉаЫЪа2017-2018бЇФъАЫФъМЖЩЯбЇЦкЦкФЉПМЪдЪ§бЇЪдОэ ЬтаЭЃКЬюПеЬт
ЁїABCЪЧЕШбќШ§НЧаЮЃЌбќЩЯЕФИпЮЊ8cmЃЌУцЛ§ЮЊ40cm2ЃЌдђИУШ§НЧаЮЕФжмГЄЪЧ_______cm.
Лђ. ЁОНтЮіЁПЃЈ1ЃЉШчЭМ1ЃЌдкЁїABCжаЃЌAB=ACЃЌЁЯAЪЧШёНЧЃЌBDЪЧACБпЩЯЕФИпЃЌ гЩЬтвтПЩжЊЃКBD=8cmЃЌSЁїABC=BDЁЄAC=40cm2ЃЌ ЁрAC=10cm=BCЃЌ ЁрдкRtЁїABDжаЃЌгЩЙДЙЩЖЈРэПЩЕУЃКAD=ЃЈcmЃЉЃЌ ЁрDC=AC-AD=4cmЃЌ ЁрдкRtЁїBDCжаЃЌгЩЙДЙЩЖЈРэПЩЕУЃКBC=ЃЈcmЃЉЃЌ ЁрДЫЪБЁїABCЕФжмГЄ=AB+AC+BC=ЃЈ...ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКББЪІДѓАцАЫФъМЖЪ§бЇЩЯВс ЕкЦпеТ ЦНааЯпЕФжЄУї ЕЅдЊВтЪд ЬтаЭЃКНтД№Ьт
вбжЊЃКШчЭМЃЌEЁЂFЪЧЦНааЫФБпааABCDЕФЖдНЧЯпACЩЯЕФ СНЕуЃЌAE=CFЁЃ
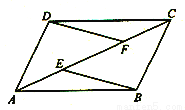
ЧѓжЄЃКЃЈ1ЃЉЁїADFЁеЁїCBE
ЃЈ2ЃЉEBЁЮDFЃЎ
ЁпЫФБпаЮABCDЮЊЦНааЫФБпаЮЃЌ ЁрADЁЮBCЃЌADЃНBC. ЁЁЁЁЁЁ(1Зж) ЁрЁЯDACЃНЁЯBCE. гжЁпAEЃНCFЃЌЁрAFЃНCE ЁрЁїADFЁеЁїCBE.ЁЁЁЁЁЁЁЁ(4Зж) ЁрЁЯAFDЃНЁЯCEB. ЁрBEЁЮDF. ЁЁЁЁЁЁЁЁЁЁЁ(6Зж ЁОНтЮіЁПЪдЬтЗжЮіЃКвЊжЄЁїADFЁеЁїCBEЃЌвђЮЊAE=CFЃЌдђСНБпЭЌЪБМгЩЯEFЃЌЕУЕНAF=CEЃЌгжвђЮЊAB...ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКББЪІДѓАцАЫФъМЖЪ§бЇЩЯВс ЕкЦпеТ ЦНааЯпЕФжЄУї ЕЅдЊВтЪд ЬтаЭЃКЬюПеЬт
вбжЊЃЌШчЭМЃЌдкЁїABCжаЃЌBOКЭCOЗжБ№ЦНЗжЁЯABCКЭЁЯACBЃЌЙ§OзїDEЁЮBCЃЌЗжБ№НЛABЁЂACгкЕуDЁЂEЃЌШєBD+CE=5ЃЌдђЯпЖЮDEЕФГЄЮЊ________ЃЎ
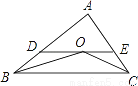
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКББЪІДѓАцАЫФъМЖЪ§бЇЩЯВс ЕкЦпеТ ЦНааЯпЕФжЄУї ЕЅдЊВтЪд ЬтаЭЃКЕЅбЁЬт
ЯТСаЬѕМўжаЃЌФмХаЖЈЁїABCЮЊжБНЧШ§НЧаЮЕФЪЧЃЈ ЃЉ
A. ЁЯA=2ЁЯB=3ЁЯC B. ЁЯA+ЁЯB=2ЁЯC
C. ЁЯA=ЁЯB=30Ёу D. ЁЯA= ЁЯB=
ЁЯB=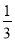 ЁЯC
ЁЯC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЫФДЈЪЁвЫБіЪа2017-2018бЇФъЩЯбЇЦкЦкФЉНЬбЇжЪСПМрВтАЫФъМЖЪ§бЇЪдОэ ЬтаЭЃКНтД№Ьт
ШЮвтвЛИіе§ећЪ§ЖМПЩвдНјааетбљЕФЗжЁОНтЮіЁП
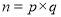 ЃЈ
ЃЈ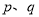 ЪЧе§ећЪ§ЃЌЧв
ЪЧе§ећЪ§ЃЌЧв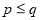 ЃЉЃЌе§ећЪ§ЕФЫљгаетжжЗжНтжаЃЌШчЙћ
ЃЉЃЌе§ећЪ§ЕФЫљгаетжжЗжНтжаЃЌШчЙћ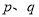 СНвђЪ§жЎВюЕФОјЖджЕзюаЁЃЌЮвУЧОЭГЦ
СНвђЪ§жЎВюЕФОјЖджЕзюаЁЃЌЮвУЧОЭГЦ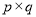 ЪЧе§ећЪ§ЕФзюМбЗжНтЃЎВЂЙцЖЈЃК
ЪЧе§ећЪ§ЕФзюМбЗжНтЃЎВЂЙцЖЈЃК 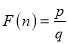 ЃЎР§Шч24ПЩвдЗжНтГЩ1ЁС24ЃЌ2ЁС12ЃЌ3ЁС8Лђ4ЁС6ЃЌвђЮЊ
ЃЎР§Шч24ПЩвдЗжНтГЩ1ЁС24ЃЌ2ЁС12ЃЌ3ЁС8Лђ4ЁС6ЃЌвђЮЊ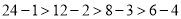 ЃЌЫљвд4ЁС6ЪЧ24ЕФзюМбЗжНтЃЌЫљвд
ЃЌЫљвд4ЁС6ЪЧ24ЕФзюМбЗжНтЃЌЫљвд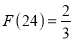 ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ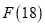 ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШчЙћвЛИіСНЮЛе§ећЪ§ЃЌ 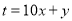 ЃЈ
ЃЈ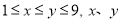 ЮЊздШЛЪ§ЃЉЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МѕШЅдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФВюМЧЮЊ
ЮЊздШЛЪ§ЃЉЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МѕШЅдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФВюМЧЮЊ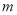 ЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МгЩЯдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФКЭМЧЮЊ
ЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МгЩЯдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФКЭМЧЮЊ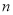 ЃЌШє
ЃЌШє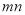 ЮЊ4752ЃЌФЧУДЮвУЧГЦетИіЪ§ЮЊЁАзюУРЪ§ЁБЃЌЧѓЫљгаЁАзюУРЪ§ЁБЃЛ
ЮЊ4752ЃЌФЧУДЮвУЧГЦетИіЪ§ЮЊЁАзюУРЪ§ЁБЃЌЧѓЫљгаЁАзюУРЪ§ЁБЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЫљЕУЁАзюУРЪ§ЁБжаЃЌЧѓ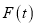 ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЫФДЈЪЁвЫБіЪа2017-2018бЇФъЩЯбЇЦкЦкФЉНЬбЇжЪСПМрВтАЫФъМЖЪ§бЇЪдОэ ЬтаЭЃКЕЅбЁЬт
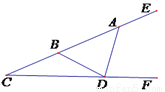
ШчЭМЃЌдк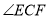 ЕФСНБпЩЯгаЕу
ЕФСНБпЩЯгаЕу ЃЌ
ЃЌ 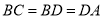 ЃЌЧв
ЃЌЧв ЃЌдђ
ЃЌдђ ЕФЖШЪ§ЮЊЃЈ ЃЉ
ЕФЖШЪ§ЮЊЃЈ ЃЉ
A. 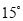 B.
B. 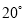 C.
C. 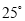 D.
D. 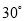
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКББЪІДѓАцЪ§бЇОХФъМЖЩЯВсЕквЛеТЬиЪтЦНааЫФБпаЮЕкЖўНкЁЖОиаЮЕФаджЪгыХаЖЈЁЗПЮЪБСЗЯА ЬтаЭЃКЕЅбЁЬт
ШєОиаЮЕФвЛЬѕЖдНЧЯпгывЛБпЕФМаНЧЪЧ40ЁуЃЌдђСНЬѕЖдНЧЯпЫљМаЕФШёНЧЕФЖШЪ§ЮЊЃЈ ЃЉ
A. 80Ёу B. 60Ёу C. 45Ёу D. 40Ёу
A ЁОНтЮіЁПЪдЬтЗжЮіЃКШчЭМЃК ИљОнЬтвтПЩЕУЃКЁЯ1=40ЁуЃЌЁпЫФБпаЮABCDЪЧОиаЮЃЌЁрOB=OCЃЌЁрЁЯOBC=ЁЯ1=40ЁуЃЌдђЁЯAOB=2ЁЯ1=80ЁуЃЎ ЙЪбЁAЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com