练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知∠D=∠A，EF∥BC，那么要使△ABC≌△DEF，给出的条件可以是（ ）

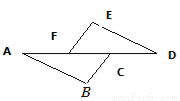
    A. ∠E=∠B B. ED=BC C. AB=EF D. AF=CD

    D 【解析】因为EF∥BC，所以∠EFD=∠BCA. A.只是三个角相等，不能得到这两个三角形全等，错误； B.相等的角所对的边不一定相等，错误； C.相等的角所对的边不一定相等，错误； D.由AF=CD，得AC=DF可得△ABC≌△DEF. 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    铅笔每支m元，小明用10元钱买了n支铅笔后，还剩下 元.

    10-mn 【解析】试题解析：由题意，买笔花费 元，则应剩下 元.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（2）练习 题型：解答题

    如图，MP切⊙O于点M，直线PO交⊙O于点A、B，弦AC∥MP，求证：MO∥BC．

    证明见解析. 【解析】证MO∥BC，只需证明同位角∠ANO=∠C即可．

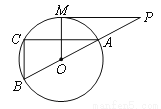
    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学 第十二章 全等三角形 检测题（附答案） 题型：解答题

    如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．

    （1）求证：△ABE≌△DCE；

    （2）当∠AEB=50°，求∠EBC的度数？

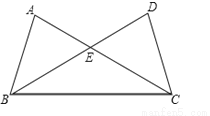
    （1）证明见解析；（2）∠EBC=25°． 【解析】试题分析：（1）根据AAS即可推出△ABE和△DCE全等； （2）根据三角形全等得出EB=EC，推出∠EBC=∠ECB，根据三角形的外角性质得出∠AEB=2∠EBC，代入求出即可． 试题解析：（1）∵在△ABE和△DCE中 ∴△ABE≌△DCE（AAS）； （2）∵△ABE≌△DCE， ∴BE=EC， ∴...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学 第十二章 全等三角形 检测题（附答案） 题型：单选题

    在△ABC中， ∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB于点E，AB=18cm，则△DBE的周长为（ ）

    A. 16cm B. 8cm C. 18cm D. 10cm

    C 【解析】因为 ∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB，易证△ACD≌△AED， 所以AE=AC=BC，ED=CD. △DBE的周长=BE+DE+DB=BE+CD+DB=BE+BC=BE+AE=AB. 因为AB=12，所以△DBE的周长=12. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：同步练习3：1.1菱形的性质与判定 题型：填空题

    菱形ABCD中，AC、BD相交于O点，若∠OBC=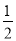∠BAC，则菱形的四个内角的度数为____________.

    60°,120°,60°,60°. 【解析】如图所示, 因为菱形对角线平分一组对角,所以∠BAC=∠BAD, ∠OBC=∠ABC, 因为∠OBC=∠BAC, 所以∠ABC=∠BAC, 所以∠ABO=∠BAO, 因为∠AOB=90°, 所以∠ABO=30°, ∠BAO=60°, 所以∠ABC=60°, ∠BAD=120°, 故答案为:60°,12...

    查看答案和解析>>

    科目：初中数学 来源：同步练习3：1.1菱形的性质与判定 题型：单选题

    菱形的边长是2 cm，一条对角线的长是2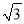 cm,则另一条对角线的长是（ ）

    A. 4 cm B. 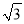cm C. 2 cm D. 2 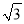cm

    C 【解析】如图所示,已知AB=2cm,因为菱形对角线互相平分,所以BO=OD=cm, 在Rt△ABO中, ,AB=2cm,BO=cm,所以AO=1cm, 故菱形的另一条对角线AC长为2AO=2cm,故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版（贵州）八年级数学下册：期末综合检测 题型：解答题

    解答下列各题.

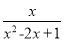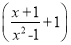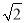    (1)先化简,再求值: ÷,其中x=+1.

    (2)分解因式:8(x2-2y2)-x(7x+y)+xy.

    (3)解不等式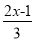≤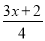-1,并把解集表示在数轴上.

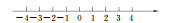
    (4)解不等式组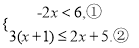并将解集在数轴上表示出来.

    (5)解方程: 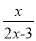+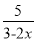=4.

    (1)原式=,当x=+1时,原式=；(2)原式=(x+4y)(x-4y)；(3)不等式的解集为x≥2，解集在数轴上表示见解析；（4）不等式组的解集为-3

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷（含解析） 题型：单选题

    下列图形中不是轴对称图形的是（ ）．

    A. 线段 B. 角 C. 等腰三角形 D. 直角三角形

    D 【解析】A选项：线段是轴对称图形，对称轴是线段的中垂线； B选项：角是轴对称图形，对称轴是其角平分线； C选项：等腰三角形是轴对称图形，对称轴是其底边上的高； D选项：直角三角形不是轴对称图形. 故选D.

    查看答案和解析>>

    同步练习册答案