
����ABCD�У�AC��BD�ཻ��O�㣬����OBC=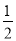 ��BAC�������ε��ĸ��ڽǵĶ���Ϊ____________.
��BAC�������ε��ĸ��ڽǵĶ���Ϊ____________.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�Ϫ��2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
�������ʽ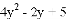 ��ֵ��7����ô����ʽ
��ֵ��7����ô����ʽ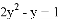 ��ֵ���ڣ� ��
��ֵ���ڣ� ��
(A)2 (B)3 (C)-2 (D)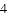
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 24.2.2ֱ�ߺ�Բ��λ�ù�ϵ��2����ϰ ���ͣ���ѡ��
Բ��һ��P��PA��PB�ֱ��С�O��A��B��CΪ�Ż�AB��һ�㣬����ACB=a�����APB=�� ��
A. 180��- 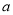 B. 90��-
B. 90��- 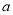 C. 90��+
C. 90��+ 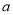 D. 180��-2
D. 180��-2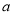
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶��ѧ ��ʮ���� ȫ�������� ����⣨���𰸣� ���ͣ������
��ͼ����֪��B��C��F��E��ͬһֱ���ϣ���1=��2��BC=EF��Ҫʹ��ABC�ա�DEF����������һ��������������������� ����ֻ��д��һ����
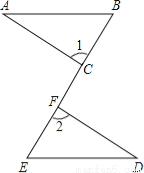
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶��ѧ ��ʮ���� ȫ�������� ����⣨���𰸣� ���ͣ���ѡ��
��֪��D=��A��EF��BC����ôҪʹ��ABC�ա�DEF�����������������ǣ� ��
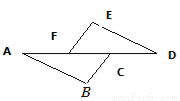
A. ��E=��B B. ED=BC C. AB=EF D. AF=CD
D ����������ΪEF��BC�����ԡ�EFD=��BCA. A.ֻ����������ȣ����ܵõ�������������ȫ�ȣ����� B.��ȵĽ����Եı߲�һ����ȣ����� C.��ȵĽ����Եı߲�һ����ȣ����� D.��AF=CD����AC=DF�ɵá�ABC�ա�DEF. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ͬ����ϰ3��1.1���ε��������ж� ���ͣ������
�жϣ�һ��Ϊ60���ƽ���ı��������Σ� ��
�� �������� ����������������ε��ж����ٶ��壺һ���ڱ���ȵ�ƽ���ı��������Σ����ı���ȣ��۶Խ����ഹֱƽ�ֵ��ı��������ν����жϣ� ��һ������60���ƽ���ı��ε��ı߲�һ����ȣ���һ�������Σ��ʱ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 25.2���оٷ�����ʲ��� ���ͣ������
�ס��ҡ�������4��ͬѧ����һ����ë�����,Ҫ����ѡ��2��ͬѧ�����׳�����.�������¼��ĸ���:
(1)��ȷ���״��һ��,�ٴ�����3��ͬѧ�����ѡȡ1��,ǡ��ѡ����ͬѧ.
(2)���ѡȡ2��ͬѧ,��������ͬѧ.
��1���� ��2��. �������������������1������һ����3�ֵȿ����ԵĽ��������ǡ��ѡ����ͬѧ����1�֣����ݸ��ʹ�ʽ������ô𰸡� ��2�������ȫ���������������������������������Ŀ�����ߵı�ֵ��Ϊ�¼��ĸ��ʡ� �����������1����ȷ���״��һ�����ٴ�����3��ͬѧ�����ѡȡ1����ǡ��ѡ����ͬѧ�ĸ����� �� ��2���Ӽס��ҡ�������4��ͬѧ�����ѡȡ2��ͬѧ�����п��ܳ��ֵĽ����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ��棨���ݣ����꼶��ѧ�²��ĩ�ۺϼ�� ���ͣ������
������x�ķ���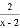 +
+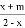 =2������,��m��ֵ����������.
=2������,��m��ֵ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ɹź��ͺ������п���ѧ�Ծ��� ���ͣ������
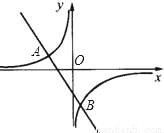
��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=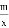 ��ͼ����A����2��1����B��1��n�����㣮
��ͼ����A����2��1����B��1��n�����㣮
��1������������һ�κ����Ľ���ʽ��
��2������ͼ��д��ʹһ�κ�����ֵ��������������ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com