练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    从正方形铁片上截去2cm宽的一个长方形，剩余矩形的面积为80cm2，则原来正方形的面积为（　　）

    A. 100cm2 B. 121cm2 C. 144cm2 D. 169cm2

    A 【解析】试题分析：设正方形边长为cm，依题意得，解方程得， （舍去）， 所以正方形的边长是10cm，面积是100cm2．故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：单选题

    二次函数y=x2+2的顶点坐标是（　　）

    A. （1，﹣2） B. （1，2） C. （0，﹣2） D. （0，2）

    D 【解析】【解析】 二次函数y=x2+2的顶点坐标是（0，2）．故选D．

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：填空题

    已知二次函数y=x2+bx+3的对称轴为x=2，则b= ．

    -4 【解析】 试题分析：可直接由对称轴公式=2，求得b=-4．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：解答题

    将进货单价40元的商品按50元出售，能卖出500个，已知这种商品每涨价1元，就会少销售10个。为了赚得8000元的利润，售价应定为多少？这时应进货多少个．

    当售价为80元时 应进200个;当售价为60元时 应进400个. 【解析】试题分析：设销售价x元/个，由于进货单价为40元的商品按50元出售时，能卖500个，已知该商品每涨价1元，其销量就要减少10个，所以现在能够卖[500-10（x-50）]个，每个利润为（x-40），而总利润为8000元，由此即可列出方程解决问题． 试题解析： 设售价定（） 元 则 售出 ， 有 ， ...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：填空题

    设有反比例函数y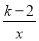＝，（x1，y1），（x2，y2）为函数图象上两点，当x1＜0＜x2时，有y1＞y2，则的k的取值范围是 ．

    k＜2 【解析】试题分析：根据题意可得，反比例函数经过二、四象限，则k－2＜0，则k＜2.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：单选题

    已知反比例函数y=﹣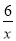，下列各点中，在其图象上的有（　　）

    A. （﹣2，﹣3） B. （2，3） C. （2，﹣3） D. （1，6）

    C 【解析】∵反比例函数y=﹣中，k=﹣6， ∴只需把各点横纵坐标相乘，结果为﹣6的点在函数图象上， 四个选项中只有C选项符合， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：解答题

    如图，笔直的公路上A、B两点相距25km，C、D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA=15km，CB=10km，现在要在公路的AB段上建一个土特产品收购站E，使得C、D两村到收购站E的距离相等，则收购站E应建在离A点多远处？

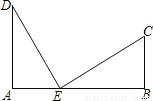
    收购站E应建在离A点10km处． 【解析】试题分析：根据C、D两村到E站的距离相等，可得DE=CE，在Rt△AED和Rt△EBC中，根据勾股定理可得AE2+AD2=BE2+BC2，设AE=x，则BE=25﹣x，列出方程，解方程求得x的值，即可得收购站E离A点的距离. 试题解析： ∵使得C，D两村到E站的距离相等． ∴DE=CE， ∵DA⊥AB于A，CB⊥AB于B， ...

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：单选题

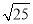    的算术平方根是（　　）

    A. 5 B. ﹣5 C. 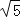D.

    C 【解析】∵=5， ∴5的算术平方根是 ， 故选C.

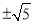
    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：解答题

    已知：如图，∠2是△ABC的一个外角．

    求证：∠2=∠A+∠B．

    证明：如图，

    ∵∠A+∠B+∠1=180° （ ）

    ∠1+∠2=180° （ ）

    ∴∠2=∠A+∠B （ ）

    三角形内角和定理；邻补角的定义；等量代换 【解析】试题分析：根据三角形内角和定理和平角的定义得出∠A+∠B+∠1=180°，∠1+∠2=180°，从而得出∠A+∠B+∠1=∠1+∠2，即∠2=∠A+∠B． 试题解析：证明：∵∠A+∠B+∠1=180°(三角形内角和定理)， ∠1+∠2=180°(邻补角的定义)， ∴∠2=∠A+∠B(等量代换)． 故答案为：三角形内角和...

    查看答案和解析>>

    同步练习册答案