练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知方程x2-6x+q=0可以配方成（x-p）2=7的形式，那么x2-6x+q=2可以配方成下列的（ ）

    A. （x-p）2=5 B. （x-p）2=9 C. （x-p+2）2=9 D. （x-p+2）2=5

    B 【解析】x2－6x＋q＝0,由题意，方程可配方成(x－p)2＝7的形式 ，所以(x－p)2-7=0,由 x2－6x＋q＝2, (x－p)2-7=2,所以 所以(x－p)2＝9，所以选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：单选题

    已知x1、x2是关于x的一元二次方程x2－(2m＋3)x＋m2＝0的两个不相等的实数根，且满足x1＋x2＝m2，则m的值是(　　)

    A. －1 B. 3 C. 3或－1 D. －3或1

    B 【解析】试题解析：根据题意得△=（2m+3）2-4m2＞0，解得m＞-； 根据根与系数的关系得x1+x2=2m+3， 则2m+3=m2， 整理得m2-2m-3=0，即（m-3）（m+1）=0， 解得m1=3，m2=-1， 则m=3．

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：填空题

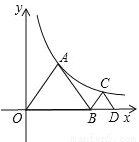
    如图，等边△OAB和等边△BCD的顶点A、C分别在双曲线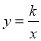的图象上，若OA=1，则点C的坐标为____________．

    （， ）． 【解析】过A作AE⊥OB于E，过C作CF⊥BD于F， ∵△OAB是等边三角形， ∴∠AOB=∠OAB=60°，OB=OA=1， ∴OE=，AE=， ∴k=， ∴双曲线的解析式为y=， 设等边三角形CBD的边长为2a， ∴BF=a，CF=a， ∴C（1+a， a）， ∴（1+a）•a =， ∴a=，（负值舍去）， ∴...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：填空题

    若一个矩形的周长为34 cm，面积是70 cm2，要求它的边长，则可设一边长为x cm，则它的邻边长为________cm，可列出方程为________，它的两条邻边的边长分别为________．

    ，(17-x)x=70，7，10 【解析】则可设一边长为x cm，则它的邻边长为cm，可列出方程为(17-x)x=70，解得,它的两条邻边的边长分别为7,10.

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：单选题

    两年内某校办工厂的利润由5万元增长到9万元，设每年利润的平均增长率为x，可以列方程得 ： (　　)

    A. 5(1＋x)＝9 B. 5(1＋x)2＝9

    C. 5(1＋x)＋5(1＋x)2＝9 D. 5＋5(1＋x)＋5(1＋x)2＝9

    B 【解析】由题意知，5(1＋x)2＝9.所以选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：解答题

    佳佳果品店在批发市场购买某种水果销售,第一次用1 200元购进若干千克,并以8元/kg出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1 452元所购买的数量比第一次多20 kg,以9元/kg售出100 kg后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.

    (1)第一次水果的进价是每千克多少元?

    (2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?

    （1）每千克6元；（2）盈利了,共盈利了388元 【解析】试题分析：（1）首先设第一次的单价为x元，则第二次单价为1．1x，根据数量=总价÷单价分别求出两次的数量，然后根据第二次的数量比第一次数量多20千克列出分式方程进行求解，最后进行验根；（2）分别求出两次的盈亏情况，然后进行合并计算． 试题解析：（1）设第一次购买的单价为x元，则第二次的单价为1．1x元， 根据题意得： =2...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：填空题

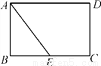
    如图，在矩形ABCD中，E是BC的中点，矩形ABCD的周长是20 cm，AE＝5 cm，则AB的长为____cm.

    4 【解析】试题分析：设AB=xcm，则由矩形ABCD的周长是20cm可得BC=10﹣xcm， ∵E是BC的中点，∴BE=BC=。 在Rt△ABE中，AE=5cm，根据勾股定理，得AB2+BE2=AE2，即x2+（）2=52，解得：x=4。 ∴AB的长为4cm。

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型：解答题

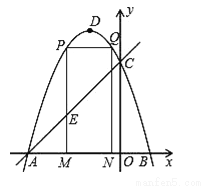
    如图，抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．

    （1）求点A、B、C的坐标；

    （2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM．如图，点P在点Q左边，试用含m的式子表示矩形PQNM的周长；

    （3）当矩形PQNM的周长最大时，m的值是多少？并求出此时的△AEM的面积；

    （4）在（3）的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG=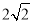DQ，求点F的坐标．

    （1）A（﹣3，0），B（1，0），C（0，3）；（2）矩形PMNQ的周长=﹣2m2﹣8m+2；（3）矩形的周长最大时，m=﹣2，S=；（4）F（﹣4，﹣5）或（1，0）． 【解析】试题分析：（1）通过解析式即可得出C点坐标，令y=0，解方程得出方程的解，即可求得A、B的坐标； （2）设M点横坐标为m，则PM=，MN=（﹣m﹣1）×2=﹣2m﹣2，矩形PMNQ的周长d=，将配方，由二次...

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上学期第二次月考数学试卷 题型：单选题

    若三角形三边分别为a、b、c，且分式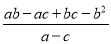的值为0，则此三角形一定是（　　）

    A. 不等边三角形 B. 腰与底边不等的等腰三角形

    C. 等边三角形 D. 直角三角形

    B 【解析】根据分式等于0的条件，分母不为0，分子等于0，即a-c≠0，ab-ac+bc-b2= ab -b2-ac+bc =b（a-b）-c（a-b）=（a-b）（b-c）=0，所以a≠c，a=b，或b=c，因此可知此三角形一定是腰与底边不等的等腰三角形. 故选：B.

    查看答案和解析>>

    同步练习册答案