
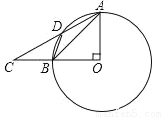
��ͼ����AOB=90�㣬C��OB���ӳ����ϣ�DΪ��O��һ�㣬��BAD=��BDC��
��1����֤��CD�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ1����OB=BC�����ı���AOBD�������
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�����ɹų����������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
�Ķ������⣺
��֪��Ϊʲô�κ�����ѭ��С��������д�ɷ�����ʽ������Ľ����̻������ԭ��ͷ�����
��1���Ķ����в��ϣ�
���⣺����һԪһ�η��̽�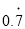 ���ɷ�����
���ɷ�����
�� 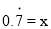 ��
��
��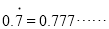 ����֪
����֪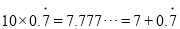 ��
��
�� 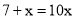 ����������Ὣ�������߶�����10�����ã�
����������Ὣ�������߶�����10�����ã�
�ɽ�� 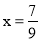 ����
���� 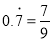 ��
��
��գ���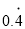 ֱ��д�ɷ�����ʽΪ_____________ ��
ֱ��д�ɷ�����ʽΪ_____________ ��
��2�����������������С��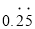 ���ɷ�����Ҫ��д������һԪһ�η��̽��н��Ĺ���.
���ɷ�����Ҫ��д������һԪһ�η��̽��н��Ĺ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ2017-2018ѧ����꼶��ѧ��ѧ����ĩ�Ծ� ���ͣ���ѡ��
��֪x1��x2�ǹ���x��һԪ���η���x2��(2m��3)x��m2��0����������ȵ�ʵ������������x1��x2��m2����m��ֵ��(����)
A. ��1 B. 3 C. 3��1 D. ��3��1
B �������������������������á�=��2m+3��2-4m2��0�����m��-�� ���ݸ���ϵ���Ĺ�ϵ��x1+x2=2m+3�� ��2m+3=m2�� ������m2-2m-3=0������m-3����m+1��=0�� ���m1=3��m2=-1�� ��m=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ� ���ͣ������
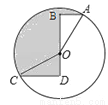
��ͼ����O�İ뾶Ϊ2����A��C�ڡ�O�ϣ��߶�BD����Բ��O����ABD=��CDB=90�㣬AB=1��CD=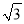 ����ͼ����Ӱ���ֵ����Ϊ______��
����ͼ����Ӱ���ֵ����Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
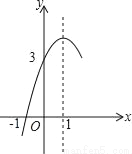
��ͼ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2��
�ڷ���ax2+bx+c=0����������x1=��1��x2=3��
��3a+c��0
�ܵ�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3
�ݵ�x��0ʱ��y��x���������
���н�����ȷ�ĸ����ǣ�������
A. 4�� B. 3�� C. 2�� D. 1��
B ���������⣺����������x����2�����㣬��b2��4ac��0�����Ԣ���ȷ�� �������ߵĶԳ���Ϊֱ��x=1�����㣨��1��0������ֱ��x=1�ĶԳƵ������Ϊ��3��0�������ax2+bx+c=0����������x1=��1��x2=3�����Ԣ���ȷ�� ��x=��=1����b=��2a����x=��1ʱ��y=0����a��b+c=0����a+2a+c=0�����Ԣ۴��� ����������x�����������Ϊ����1��0��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶���ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ������
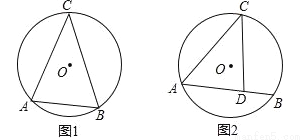
��֪����A��B��C�ڡ�O�ϣ���C=32�㣬�����̶ȵ�ֱ����ͼ��
��1����ͼ1�л���һ����58��ǵ�ֱ�������Σ�
��2����D����AB�ϣ���ͼ2�л���һ����58��ǵ�ֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶���ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ������
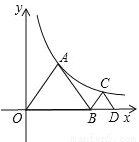
��ͼ���ȱߡ�OAB�͵ȱߡ�BCD�Ķ���A��C�ֱ���˫����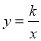 ��ͼ���ϣ���OA=1�����C������Ϊ____________��
��ͼ���ϣ���OA=1�����C������Ϊ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶����ѧ�ڶ��¡�һԪ���η��̡���Ԫ���� ���ͣ������
��һ�����ε��ܳ�Ϊ34 cm�������70 cm2��Ҫ�����ı߳��������һ�߳�Ϊx cm���������ڱ߳�Ϊ________cm�����г�����Ϊ________�����������ڱߵı߳��ֱ�Ϊ________��
��(17-x)x=70��7��10 �������������һ�߳�Ϊx cm���������ڱ߳�Ϊcm�����г�����Ϊ(17-x)x=70�����,���������ڱߵı߳��ֱ�Ϊ7,10.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������Դ��2016-2017ѧ����꼶����ĩ������ѧ�Ծ����� ���ͣ������
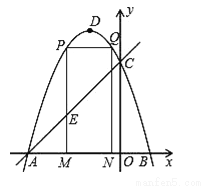
��ͼ��������y=��x2��2x+3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ��㣮
��1�����A��B��C�����ꣻ
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ����P�ڵ�Q��ߣ����ú�m��ʽ�ӱ�ʾ����PQNM���ܳ���
��3��������PQNM���ܳ����ʱ��m��ֵ�Ƕ��٣��������ʱ�ġ�AEM�������
��4���ڣ�3���������£�������PMNQ���ܳ����ʱ������DQ������������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ�������FG=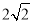 DQ�����F�����꣮
DQ�����F�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com