
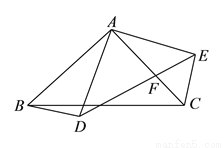
如图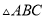 与
与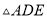 都是以
都是以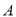 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, 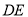 交
交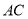 于点
于点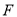 ,若
,若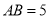 ,
, 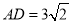 ,当
,当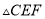 是直角三角形时,则
是直角三角形时,则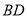 的长为__________.
的长为__________.
科目:初中数学 来源:江西省景德镇市2017-2018学年八年级上学期期末质量检测数学试卷 题型:填空题
已知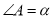 (其中
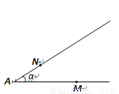
(其中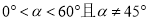 ),在∠A两条边上各任取一点分别记为M、N,并过该点分别引一条直线,并使得该直线与其所在的边夹角也为
),在∠A两条边上各任取一点分别记为M、N,并过该点分别引一条直线,并使得该直线与其所在的边夹角也为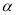 ,设两条直线交于点O,则∠MON=______________________.
,设两条直线交于点O,则∠MON=______________________.
查看答案和解析>>
科目:初中数学 来源:湖北省十堰市丹江口市2018届九年级(上)期中数学试卷 题型:解答题
已知抛物线y=x2-(m+1)x+m,
(1)求证:抛物线与x轴一定有交点;
(2)若抛物线与x轴交于A(x1,0),B(x2,0)两点,x1﹤0﹤x2,且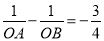 ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源:湖北省十堰市丹江口市2018届九年级(上)期中数学试卷 题型:单选题
如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
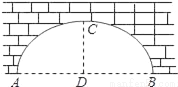
A. 6.5米 B. 9米 C. 13米 D. 15米
A 【解析】试题分析:根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O.连接OA.根据垂径定理和勾股定理求解.得AD=6设圆的半径是r, 根据勾股定理, 得r2=36+(r﹣4)2,解得r=6.5查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:解答题
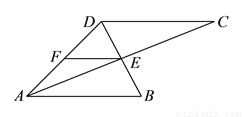
如图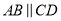 ,
, 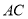 平分
平分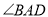 ,
, 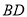 平分
平分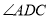 ,
, 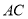 和
和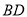 交于点
交于点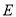 ,
, 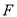 为
为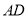 的中点,连结
的中点,连结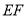 .
.
(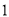 )找出图中所有的等腰三角形.
)找出图中所有的等腰三角形.
(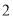 )若
)若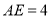 ,
, 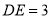 ,求
,求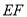 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:填空题
已知点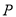 的坐标为
的坐标为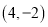 ,则点
,则点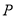 到
到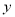 轴的距离为__________.
轴的距离为__________.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:单选题
下列定理中,没有逆定理的是( ).
A. 全等三角形对应角相等 B. 线段垂直平分线上的点到线段两端的距离相等
C. 一个三角形中,等角对等边 D. 两直线平行,同位角相等
A 【解析】A选项中,因为“对应角相等不一定是全等三角形”,所以A中定理没有有逆定理; B选项中,因为“到线段两端距离相等的点在线段的垂直平分线上”,所以B中定理有逆定理; C选项中,因为“在同一个三角形中,等边对等角”,所以C中定理有逆定理; D选项中,因为“同位角相等,两直线平行”,所以D中定理有逆定理. 故选A.查看答案和解析>>
科目:初中数学 来源:广东省广州市番禺区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若分式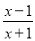 有意义,则x的取值范围是____.
有意义,则x的取值范围是____.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:解答题
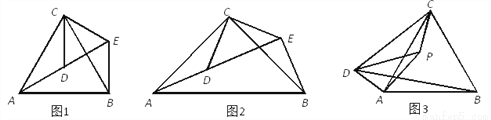
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则:
①∠BEC=_°;②线段AD、BE之间的数量关系是_.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com