
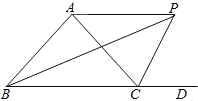
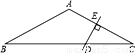
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:解答题
计算: (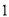 )
)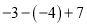 .(
.( )
)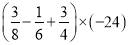 .
.
(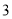 )
)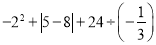 .
.
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:解答题
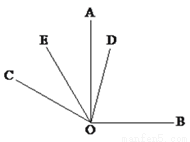
如图,已知同一平面内∠AOB=90°,∠AOC=60°.
(1)填空:∠BOC=__________;
(2)如果OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为_______;
(3)在(2)的条件下,将题目中∠AOC=60°改成∠AOC=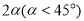 ,其它条件不变,请求出∠DOE的度数.
,其它条件不变,请求出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:单选题
已知方程x-2y+3=8,则整式x-2y的值为:
A. 5 B. 10 C. 11 D. 15
A 【解析】试题解析: 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(北师大版):期中检测题 题型:解答题
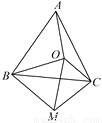
如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(北师大版):期中检测题 题型:填空题
某主题公园内一个活动项目的收费标准如下:个人票,每张10元;团体票,满20张八折优惠.当人数为________时(人数不到20人),买20人的团体票反而合算.
17,18,19 【解析】【解析】 设有x人时买20人的团体票才能比普通票便宜,根据题意得: ,解得:16<x<20,故至少17人买20人的团体票才能比普通票便宜. 故答案为:17,18,19.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(北师大版):期中检测题 题型:单选题
已知,直线l经过第二、三、四象限,l的解析式是y=(m﹣2)x+n,则m的取值范围在数轴上表示为( )
A. 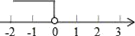 B.
B. 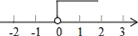
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型:填空题
如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,线段DE=1cm,则BD的长为_____.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 测试 题型:解答题
在直径为20 cm的圆中,有一条弦长为16 cm,求它所对的弓形的高.
4 cm或16 cm. 【解析】试题分析: 连接OB,利用垂径定理和勾股定理计算OC的长,即可得到弦AB所对的两个弓形的高. 试题解析: ∵这条小于直径的弦所对的弧有两条:劣弧与优弧,∴对应的弓形也有两个. 如图,HG为⊙O的直径,且HG⊥AB,AB=16 cm,HG=20 cm,连接BO. ∴OB=OH=OG=10 cm,BC=AB=8 cm.∴OC===6(...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com