
边长分别等于6 cm、8 cm、10cm的三角形的内切圆的半径为( )cm.
A. 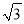 B.
B. 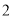 C.
C. 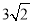 D.
D. 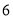
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
车辆经过某大桥收费站时, 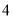 个收费通道
个收费通道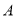 、
、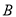 、
、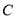 、
、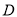 中,可随机选择其中的一个通过.
中,可随机选择其中的一个通过.
(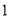 )一辆车经过此收费站时,选择
)一辆车经过此收费站时,选择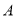 通道通过的概率是__________.
通道通过的概率是__________.
(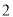 )用树状图或列表法两辆车经过此收费站时,选择不同通道通过的概率.
)用树状图或列表法两辆车经过此收费站时,选择不同通道通过的概率.
查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
将一个长方体内部挖去一个圆柱(如图所示),它的主视图是( )
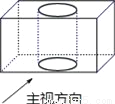
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;② 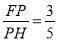 ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④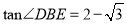 . 其中正确的是( ).
. 其中正确的是( ).
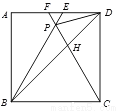
A. ①②③④ B. ①②④ C. ②③④ D. ①③④
D 【解析】分析:根据等边三角形的性质和正方形的性质,得到∠PCD=30°,于是得到∠CPD=∠CDP=75°,证得∠EDP=∠PBD=15°,于是得到△BDE∽△DPE,故①正确由于∠FDP=∠PBD,∠DFP=∠BPC=60°,推出△DFP∽△BPH,得到,故②错误;由于∠PDH=∠PCD=30°,∠DPH=∠DPC,推出△DPH∽△CPD,得到,PB=CD,等量代换得到PD2=PH•P...查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与过A点的⊙O的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
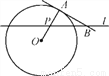
A. 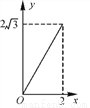 B.
B. 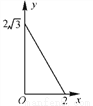 C.
C. 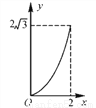 D.
D. 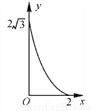
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
阅读下列解答过程,然后回答问题.已知多项式x3+4x2+mx+5有一个因式(x+1),求m的值.
【解析】
设另一个因式为(x2+ax+b),
则x3+4x2+mx+5=(x+1)(x2+ax+b)=x2+(a+1)x2+(a+b)x+b,
∴a+1=4,a+b=m,b=5,∴a=3,b=5,∴m=8;
依照上面的解法,解答问题:若x3+3x2﹣3x+k有一个因式是x+1,求k的值.
-5. 【解析】试题分析:将一个多项式化成几个单项式或单项式乘积的形式时,如果有一个因式为零时,则整个多项式的值为零.本题中假设x+1=0求出x的值,从而将x的值代入代数式求出k的值. 试题解析:∵多项式x3+4x2+mx+5有一个因式(x+1), ∴令x+1=0得x=﹣1,即当x=﹣1时,原多项式为零, ∴(﹣1)3+3×(﹣1)2﹣3×(﹣1)+k=0, ∴k=﹣...查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:填空题
已知等腰三角形的一个底角等于15°,腰长为10 cm,则它的面积是______;
25平方单位 【解析】如图: AC=AB=4cm,∠B=∠ACB=15°, 过点C作CD⊥AB于D, ∴∠CAD=∠ACB+∠B=15°+15°=30° ∴CD=AC=5cm(在直角三角形中,30°角所对的直角边是斜边的一半), ∴S△ABC=×5×10=25(cm2). ∴这个三角形的面积为25cm2. 故答案为:25cm2.查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:解答题
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.
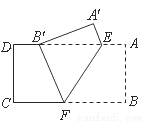
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
已知菱形的周长为4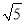 ,两条对角线的和为6,则菱形的面积为( )
,两条对角线的和为6,则菱形的面积为( )
A. 2 B. 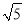 C. 3 D. 4
C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com