
�Ķ����н����̣�Ȼ��ش����⣮��֪����ʽx3+4x2+mx+5��һ����ʽ��x+1������m��ֵ��
��������
����һ����ʽΪ��x2+ax+b����
��x3+4x2+mx+5=��x+1����x2+ax+b��=x2+��a+1��x2+��a+b��x+b��
��a+1=4��a+b=m��b=5����a=3��b=5����m=8��
��������Ľⷨ��������⣺��x3+3x2��3x+k��һ����ʽ��x+1����k��ֵ��
-5. �������������������һ������ʽ���ɼ�������ʽ����ʽ�˻�����ʽʱ�������һ����ʽΪ��ʱ������������ʽ��ֵΪ��.�����м���x+1=0���x��ֵ���Ӷ���x��ֵ�������ʽ���k��ֵ. ����������߶���ʽx3+4x2+mx+5��һ����ʽ��x+1���� ����x+1=0��x=��1������x=��1ʱ��ԭ����ʽΪ�㣬 �ࣨ��1��3+3������1��2��3������1��+k=0�� ��k=��... ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭������������ʮ����ѧ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��һ�麬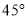 �ǵ�ֱ�����ǰ壬����һ����Ƕ���
�ǵ�ֱ�����ǰ壬����һ����Ƕ���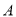 �ڰ뾶Ϊ
�ڰ뾶Ϊ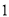 �ġ�
�ġ�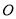 �ϣ���
�ϣ���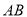 ��
�� 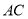 �ֱ����
�ֱ����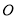 ���ڵ�
���ڵ�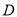 ��
�� 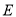 ����
���� �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С����÷� ���ͣ������
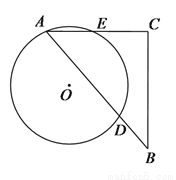
��ͼ����һ�ŵ��Թ��̵ı��棬����Բ�Ķ���O����Բ����AB���ڵ�ֱ����СԲ�����ߣ��е�ΪC����֪��Բ�İ뾶Ϊ5cm��СԲ�İ뾶Ϊ1cm������AB�ij��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С����÷� ���ͣ���ѡ��
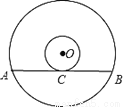
��ͼ����ƽ��ֱ������ϵ�У���ABC��ijһ��P��תһ���ĽǶȵõ���A��B��C�䣬����ͼ�α任ǰ��Ĺ�ϵ�ɵõ�P������Ϊ�� ��.
A����0��1�� B����1����1�� C����0����1�� D����1��0��
B�� �������� �����������������ṹ���ҳ���Ӧ�����ߵĴ�ֱƽ���ߵĽ��㼴Ϊ��ת���ģ���ͼ�ο�֪����Ӧ�������CC�䡢AA��Ĵ�ֱƽ���ߵĽ����ǵ㣨1����1����������ת�任�����ʣ��㣨1����1����Ϊ��ת���ģ� ����ת����������P��1����1������ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С����÷� ���ͣ���ѡ��
�߳��ֱ����6 cm��8 cm��10cm�������ε�����Բ�İ뾶Ϊ�� ��cm.
A. 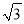 B.
B. 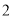 C.
C. 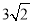 D.
D. 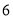
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ߺ��н�������2017-2018ѧ�����ѧ�ڰ��꼶�ڶ����¿� ���ͣ������
��ƽ��ֱ������ϵxOy�У���֪��A��2��3����������������һ��P��ʹ�á�AOP�ǵ��������Σ��������ĵ�P����______����
8 �������������������x����������y����������ϸ���2������x��ĸ������y��ĸ������ϸ���1�����ܼ���6��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ߺ��н�������2017-2018ѧ�����ѧ�ڰ��꼶�ڶ����¿� ���ͣ���ѡ��
��ͼ����֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F����������������ۣ��١�PFA�ա�PEB����EF=AP���ۡ�PEF�ǵ���ֱ�������Σ��ܵ���EPF�ڡ�ABC���ƶ���P��תʱ����E����A��B�غϣ���S�ı���AEPF=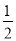 S��ABC������������ʼ����ȷ�� ��������
S��ABC������������ʼ����ȷ�� ��������
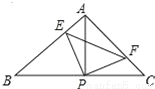
A. 1�� B. 2�� C. 3�� D. 4��
C ����������AB=AC����BAC=90�㣬P��BC�е㣬 ��AP��BC��AP=PB�� ��B=��CAP=45�㣬 �ߡ�APF+��FPA=90�㣬 �� APF+��BPE=90�㣬 ���APF=��BPE�� �ڡ�BPE�͡�APF�У� ��B=��CAP�� BP=AP����BPE =��APF�� ���PFA�ա�PEB���ʢ���ȷ�� �ߡ�ABC�ǵ���ֱ������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��㶫ʡ��ݸ�����dz�ѧУ����ѧģ���Ծ� ���ͣ������
�ⲻ��ʽ�飺  ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�괺�˽̰���꼶��ѧ�²ᣨ���������в��� ���ͣ���ѡ��
����?ABCD����������ȷ���ǣ�������
A. ��AB��BC����?ABCD������ B. ��AC��BD����?ABCD��������
C. ��AC=BD����?ABCD�Ǿ��� D. ��AB=AD����?ABCD��������
C ��������ѡ��C�У�������ε��ж��������Խ�����ȵ�ƽ���ı����Ǿ��Σ�����ѡC.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com