
用配方法解方程x2+10x+9=0,下列变形正确的是( )
A. (x+5)2=16 B. (x+10)2=91
C. (x﹣5)2=34 D. (x+10)2=109
A 【解析】x2+10x+9=0, (x+5)2+25=-9+25, (x+5)2=16.故选A. 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
在实数π、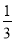 、
、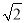 、0.1234中,无理数的个数为( )
、0.1234中,无理数的个数为( )
A. 1 B. 2 C. 3 D. 4
B 【解析】根据无理数的概念,无限不循环小数是无理数,可知π、是无理数. 故选:B.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
如图,AB为⊙O的直径,点C在⊙O上,若∠C=16°,则∠BOC的度数是( )
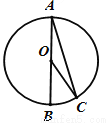
A. 74° B. 48° C. 32° D. 16°
C 【解析】∵OA=OC, ∴∠A=∠C=16°, ∴∠BOC=∠A+∠C=32°. 故选C。查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:填空题
在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,以PB为边作等边△PBM,则线段AM的长最大值为_____.
5. 【解析】如图,将三角形APM绕着P点旋转60°,得DPB,连接AD,则DP=AP,∠APD=60°,AM=BD, ADP是等边三角形,所以BDAD+AB可得,当D在BA延长线上时,BD最长,点D与O重合,又点A的坐标为(2,0),点B的坐标为(5,0),AB=3,AD=AO=2, BD=AD+AB=5=AM,所以AM最大值是5. 故答案为5.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(﹣1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )
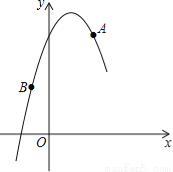
A. (﹣2,0) B. (0.5,6.5) C. (3,2) D. (2,2)
C 【解析】试题分析:因为抛物线过A(2,5),B(﹣1,2)两点,所以把以上两点的坐标代入求出a和b的值即可求出抛物线的解析式,然后分别把A、B、C、D点的横坐标代入解析式即可判定. 【解析】 把A(2,5),B(﹣1,2)两点坐标代入得, 解这个方程组,得, 故抛物线的解析式为y=﹣x2+2x+5; 当x=﹣2时,y=﹣3,x=0.5时,y=,x=3时,y=2,...查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据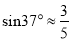 ,
, 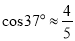 ,
, 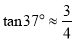 )
)

查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
已知直角坐标内,半径为2的圆心坐标为(3,-4),当该圆向上平移m个单位长度时,若要此圆与x轴没有交点,则m的取值范围是 _______________.
m<2或m>6 【解析】圆心向上平移m个单位长度后坐标为(3,m-4), ∵圆与x轴没有交点, ∴所以圆心到x轴的距离>2, 即m-4>2或m-4<-2, ∴m>6或m<2. 故答案为m>6或m<2.查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
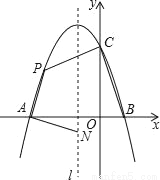
如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
下列运算正确的是( )
A. 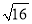 =8 B.
=8 B. 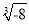 =﹣2 C.
=﹣2 C. 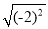 =﹣2 D.
=﹣2 D. 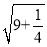 =3+
=3+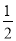
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com