
在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,以PB为边作等边△PBM,则线段AM的长最大值为_____.
5. 【解析】如图,将三角形APM绕着P点旋转60°,得DPB,连接AD,则DP=AP,∠APD=60°,AM=BD, ADP是等边三角形,所以BDAD+AB可得,当D在BA延长线上时,BD最长,点D与O重合,又点A的坐标为(2,0),点B的坐标为(5,0),AB=3,AD=AO=2, BD=AD+AB=5=AM,所以AM最大值是5. 故答案为5. 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①abc<0;②当x=1时,函数有最大值.③当x=﹣1或x=3时,函数y的值都等于0.④4a+2b+c<0.其中正确结论的个数是( )
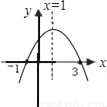
A. 1 B. 2 C. 3 D. 4
C 【解析】根据函数图象,我们可以得到以下信息:a<0,c>0,对称轴x=1,b>0,与x轴交于(-1,0)(3,0)两点.①abc<0,正确;②当x=1时,函数有最大值,正确;③当x=-1或x=3时,函数y的值都等于0,正确;④当x=2时,y=4a+2b+c>0,错误; 故选:C.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
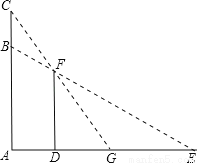
如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
方程x2-4=0的解是( )
A. x=2 B. x=-2 C. x=±2 D. x=±4
C 【解析】试题分析:方程变形为x2=4,再把方程两边直接开方得到x=±2. 【解析】 x2=4, ∴x=±2. 故选C.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:解答题
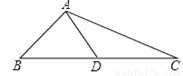
如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
已知方程x2+bx+c=0有两个相等的实数根,且当x=a与x=a+n时,x2+bx+c=m,则m、n的关系为( )
A. m=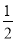 n B. m=
n B. m=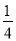 n C. m=
n C. m=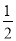 n2 D. m=
n2 D. m=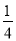 n2
n2
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
用配方法解方程x2+10x+9=0,下列变形正确的是( )
A. (x+5)2=16 B. (x+10)2=91
C. (x﹣5)2=34 D. (x+10)2=109
A 【解析】x2+10x+9=0, (x+5)2+25=-9+25, (x+5)2=16.故选A.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
一副三角板叠放如图,则△AOB与△DOC的面积之比为_____________.
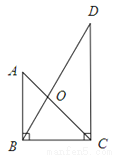
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:解答题
解不等式组: 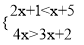 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com