
如图:△ABC中,AD平分∠BAC.DE⊥AB于点E.S△ABC=8.DE=2.AB=5则 AC=( )
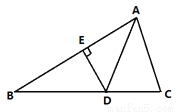
A. 4 B. 5 C. 3 D. 2
C 【解析】如图,作DF⊥AC于点F, ∵AD平分∠BAC,DE⊥AB于点E, ∴DF=DE=2. ∵S△ABD=ABDE=5,S△ABC=8, ∴S△ADC=8-5=3, 又∵S△ADC =ACDF, ∴AC=3,解得AC=3. 故选C.科目:初中数学 来源:初一数学第一学期4.1线段、直线、射线 同步练习 题型:填空题
如图,图中有__条直线,有__条射线,有__条线段,以E为顶点的角有__个.
查看答案和解析>>
科目:初中数学 来源:2018年春九年级数学下册湘教版:单元测试(四) 概率 题型:解答题
下列事件,哪些是必然事件,哪些是不可能事件,哪些是随机事件?
(1)用长度分别为2 dm,3 dm,5 dm的三根钢筋,首尾相连能焊成一个三角形;
(2)如果两个角相等,那么这两个角是对顶角;
(3)任意画一个三角形,其内角和是180°.
(1)是不可能事件.(2)是随机事件.(3)是必然事件. 【解析】试题分析:(1)根据三角形的三边关系可判断; (2)根据对顶角的概念可判断; (3)根据三角形的内角和定理可判断. 试题解析:(1) 根据三角形的三边关系,两边之和大于第三边,可由2+3=5知是不可能事件. (2)根据对顶角的概念,有公共地点,一个角的两边是另一角的两边的反向延长线,故可知两角相等有可能...查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
(本题共10分)AB和AC 相交于点A, BD和CD相交于点D,探究∠BDC与∠B 、 ∠C、∠BAC的关系.
小明是这样做的:
解:以点A为端点作射线AD.
∵∠1是△ABD的外角,∴∠1= ∠B+∠BAD.
同理∠2=∠C+∠CAD.
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD.即∠BDC=∠B+∠C+∠BAC.
小英的思路是:延长BD交AC于点E.
(1)按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论.

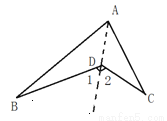
(2)按照上面的思路解决如下问题:如图:在△ABC中,BE、CD分别是∠ABC∠ACB的角平分线,交AC于E,交AB于D.BE、CD相交于点O,∠A=60°.求∠BOC的度数.
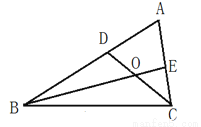
(3)如图:△ABC中,BO、CO分别是∠ABC与∠ACB的角平分线,且BO、CO相交于点O.猜想∠BOC与∠A有怎样的关系,并加以证明.
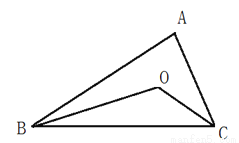
查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
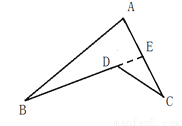
如图:在△ABC中,∠ABC=45°,AD、BE是△ABC 的高,若已知CD=5,就可得到DF=5,这样做的理论依据_________________________.
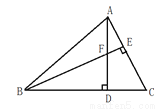
查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,在△ABC中,AB=AC,D为 BC 的中点,连接AD,那么以下结论不正确的是( )
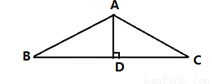
A. △ABD≌△ACD B. ∠B=∠C
C. AD是△ABC的高 D. AD不是△ABC的角平分线
D 【解析】∵在△ABC中,AB=AC,D为BC中点, ∴∠B=∠C,AD⊥BC,AD平分∠BAC, ∴AD是△ABC的高,△ABD≌△ACD(HL), 由此可知选项A、B、C都是正确的,只有D是错误的. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:3.9 弧长及扇形的面积 题型:填空题
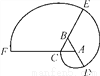
如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中 的圆心依次是A、B、C,如果AB=1,那么曲线CDEF的长是 .
的圆心依次是A、B、C,如果AB=1,那么曲线CDEF的长是 .
查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.1 二次函数 题型:单选题
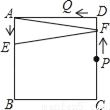
如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( )
A. 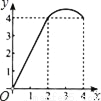 B.
B. 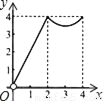 C.
C. 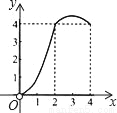 D.
D. 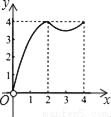
查看答案和解析>>
科目:初中数学 来源:人教七年级下册数学第九章-不等式与不等式组单元测试 题型:解答题
x为何值时,代数式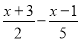 的值是非负数?
的值是非负数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com