
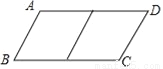
�ڱ߲���ȵ�ƽ���ı���ֽƬ����ȥһ�����Σ�����һ���ı��Σ���Ϊ��һ�β����������µ��ı���ֽƬ���ټ�ȥһ�����Σ���ʣ��һ���ı��Σ���Ϊ�ڶ��β��������������ƣ�����n�β��������µ��ı��������Σ����ԭƽ���ı���Ϊn�����Σ����磺��ͼ1��?ABCD�У���AB=1��BC=2����?ABCDΪ1�����Σ�
��1���������жϣ�
�ڱ߳��ֱ�Ϊ1��3��ƽ���ı������� �������Σ�
�ڱ߳��ֱ�Ϊ3��4��ƽ���ı������� �������Σ�
��2��������̽������㣺
����֪?ABCD���ڱ߳��ֱ�Ϊ2��a��a��2��������3�����Σ��뻭��?ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�д��a��ֵ��
����֪?ABCD���ڱ߳��ֱ�Ϊa��b��a��b��������a=7b+r��b=4r����д��?ABCD�Ǽ������Σ�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2016-2017�����꼶������ĩ��ѧ�Ծ� ���ͣ������
���㣺
(1)( 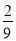 ��
��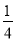 ��
��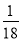 )��(��
)��(��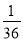 ); (2)��14��(��6)��2��3��(��
); (2)��14��(��6)��2��3��(��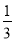 )��
)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��������2018����꼶����ĩģ����ѧ�Ծ��������棩 ���ͣ���ѡ��
��ͼ����֪DE��FG��BC���ҽ���ABC�ֳ������ȵ������֣���BC=15����FG�ij����ǣ� ��
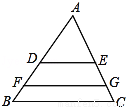
A. 5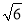 B. 10 C. 4
B. 10 C. 4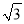 D. 7.5
D. 7.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�괺�˽̰����꼶��ѧ�²ᣨ��������ĩ���� ���ͣ���ѡ��
ij�̵��ϰ�����һ����Ʒ����Ҫ�Բ����ڽ���20%��������ۣ���Ϊ�˻�ø�����������Ը߳�����80%�ļ۸��ۣ����������±��Ϊ360Ԫ��������Ʒ���̵��ϰ��ü۵������Ϊ(����)
A. 82Ԫ B. 100Ԫ C. 120Ԫ D. 160Ԫ
C ���������������a,�ϰ��ü��������y, �������a(1+80%)=360,���a=200, y=360-a(1+20%)=360-200(1+20%)=360-240=120. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�괺�˽̰����꼶��ѧ�²ᣨ��������ĩ���� ���ͣ���ѡ��
����˵������ȷ����( )
A. 4��16������ƽ���� B. 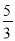 ��
��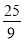 ��һ��ƽ����
��һ��ƽ����
C. (��6)2��ƽ������6 D. (��3)3����������3
C �����������������A����Ϊ42��16������4��16������ƽ��������ȷ�� B����Ϊ�����Ե�ƽ�����ǡ��������ǵ�һ��ƽ��������ȷ�� C������6��2��36��36��ƽ�����ǡ�6��������� D��(��3)3����������3��ȷ�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����д�����2018����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ������
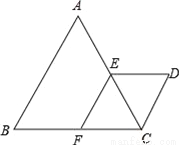
��ͼ��ABC���CDE���ǵȱ������Σ���E��F�ֱ���AC��BC�ϣ���EF��AB��
��1����֤���ı���EFCD�����Σ�
��2����CD=4����D��F�����ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����д�����2018����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ������
��֪���������Խ��ߵij��ֱ�Ϊ5cm��8cm����������ε������_____cm2��
20 ����������������� ����֪��,������� �ʴ�Ϊ:20.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���B���� ���ͣ������
��֪һԪ���η���mx2��2mx��m��2��0��
(1)����������������ʵ��������m��ȡֵ��Χ��
(2)�����̵���ʵ����Ϊx1��x2����|x1��x2|��1����m��ֵ��
(1) m>0��(2)8 �������������������1���ȸ��ݷ�������������ȵ�ʵ�����ó�����m�IJ���ʽ�����m��ȡֵ��Χ���ɣ� ��2�����ݷ�����ʵ��Ϊx1��x2�����x1+x2��x1•x2��ֵ���ٸ���|x1-x2|=1���ó���x1+x2��2-4x1x2=1���ٰ�x1+x2��x1•x2��ֵ������㼴�ɣ� �����������1���߹���x��һԪ���η���mx2-2mx+m-2=0������ʵ������ ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶����ĩģ����ѧ�Ծ��������棩 ���ͣ���ѡ��
������x��һԪ���η���kx2��2x��1=0����������ȵ�ʵ��������k��ȡֵ��Χ�ǣ�������
A. k����1 B. k����1��k��0 C. k��1 D. k��1��k��0
B ������������������߹���x��һԪ���η���kx2-2x-1=0����������ȵ�ʵ������ ��k��0�ҡ���0������-2��2-4��k����-1����0�� ���k��-1��k��0�� ��k��ȡֵ��ΧΪk��-1��k��0�� ��ѡB.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com