
��ƽ��ֱ������ϵ�У�������y=��2x2��ͼ��������ƽ��1����λ���ȣ�������ƽ��5����λ���ȣ�����ͼ��ĺ�������ʽ�� ��
y=2��x��1��2+5�� ������������������ɡ�����Ҽ�����ԭ���֪��������y=��2x2��ͼ������ƽ��1����λ���ú���ͼ��Ĺ�ϵʽ�ǣ�y=��2��x��1��2�� �ɡ��ϼ��¼�����ԭ���֪��������y=��2��x��1��2��ͼ������ƽ��5����λ�������ú���ͼ��Ĺ�ϵʽ�ǣ�y=2��x��1��2+5�� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ����������ѧ2017-2018ѧ����꼶1���¿���ѧ�Ծ� ���ͣ���ѡ��
һ�κ���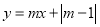 ��ͼ����㣨0��2������y��x�������������m��ֵΪ��������
��ͼ����㣨0��2������y��x�������������m��ֵΪ��������
A. ��1 B. 1 C. 3 D. ��1��3
C ����������һ�κ���y=mx+|m-1|��ͼ����㣨0��2���� ��|m-1|=2�� ��m-1=2��m-1=-2�� ���m=3��m=-1�� ��y��x����������� ��m��0�� ��m=3�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶1���¿���ѧ�Ծ� ���ͣ������
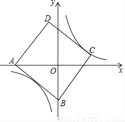
��ͼ��������ABCD�ı߳�Ϊ5����A������Ϊ����4��0������B��y���ϣ�������������y=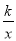 ��k��0����ͼ�����C����÷����������ı���ʽΪ_______��
��k��0����ͼ�����C����÷����������ı���ʽΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ͡������Ƭ��У2018����꼶10���¿���ѧ�Ծ� ���ͣ������
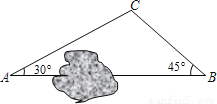
��ͼ��A��B����֮����һ��ɽ������ԭ����A�ص�B�ؾ���C��������A��C��B��ʻ���ֿ�ͨ����������ֱ����ֱ��AB��ʻ����֪AC=10ǧ�ף���A=30�㣬��B=45�㣮��������ͨ��������A�ص�B�ر�ԭ�����߶���ǧ�ף�������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ͡������Ƭ��У2018����꼶10���¿���ѧ�Ծ� ���ͣ������
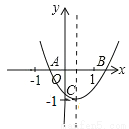
��֪�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ��OA=OC�����������ߵ�����д�����º���a��b��c������ĸ�ĵ�ʽ��ʽ����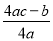 =-1����ac+b+1=0����abc>0����a-b+c>0.��ȷ�������______________.
=-1����ac+b+1=0����abc>0����a-b+c>0.��ȷ�������______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ͡������Ƭ��У2018����꼶10���¿���ѧ�Ծ� ���ͣ���ѡ��
��P1(��1��y1)��P2(3��y2)��P3(5��y3)���ڶ��κ���y����x2��2x��c��ͼ���ϣ���y1��y2��y3�Ĵ�С��ϵ��(����)
A. y3��y2��y1 B. y3��y1��y2 C. y1��y2��y3 D. y1��y2��y3
D ����������y=?x2+2x+c�� ��Գ���Ϊx=1�� P2(3,y2),P3(5,y3)�ڶԳ�����Ҳ࣬y��x���������С�� ��3<5�� ��y2>y3�� ���ݶ��κ���ͼ��ĶԳ��Կ�֪,P1(?1,y1)��(3,y1)���ڶԳ���Գƣ� ��y1=y2>y3�� ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ��������̨��2018����꼶���ϣ���һѧ����ѧ�Ծ� ���ͣ������
ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ����Ӫ���η��֣������۵�����25Ԫʱ��ÿ���������Ϊ250�������۵���ÿ����1Ԫ��ÿ����������ͼ���10����
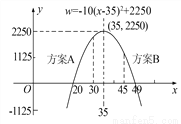
(1)д���̳��������ֹ��ߣ�ÿ�����õ���������w(Ԫ)�����۵���x(Ԫ)֮��ĺ�����ϵʽ��
(2)�����۵���Ϊ����Ԫʱ�����ľ�ÿ��������������
(3)�̳���Ӫ���������������������A��B����Ӫ��������
����A�����ľߵ����۵��۸��ڽ����Ҳ�����30Ԫ��
����B��ÿ��������������10������ÿ���ľߵ���������Ϊ25Ԫ��
��Ƚ����ַ��������������ߣ���˵�����ɣ�
��1��w����10x2��700x��10000�� ��2�����۵���Ϊ35Ԫʱ��ÿ��������������������Ϊ2250Ԫ�� ��3������A�����������ߣ����ɼ�����. �������������������1����������=�����۵���-���ۣ������������г�������ϵʽ���ɣ� ��2�����ݣ�1��ʽ�г��ĺ�����ϵʽ�������䷽�������ֵ�� ��3���ֱ��������A��B��x��ȡֵ��Χ��Ȼ��ֱ����A��B�������������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ��������̨��2018����꼶���ϣ���һѧ����ѧ�Ծ� ���ͣ���ѡ��
����x2+3x��6=0��x2��6x+3=0���и��ij˻����ڣ�������
A. ��18 B. 18 C. ��3 D. 3
A ������������������ɸ���ϵ���Ĺ�ϵ�ɵã�����x2+3x-6=0�������ij˻���-6��x2-6x+3=0�������ij˻���3�����Է���x2+3x-6=0��x2-6x+3=0���и��ij˻�=-6��3=-18����ѡ��A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ��ʦ��棩�����м���� ���ͣ������
x��y��ƽ����һ���ǷǸ������ò���ʽ��ʾΪ____��
x2��y2��0 ���������������� x��y��ƽ����һ���ǷǸ������ò���ʽ��ʾΪx2��y2��0���ʴ�Ϊ��x2��y2��0���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com