
如图, 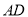 是
是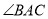 的平分线,点
的平分线,点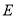 在
在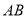 上,且
上,且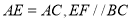 交
交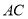 于点
于点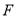 .试说明:
.试说明: 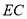 平分
平分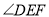 .
.
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
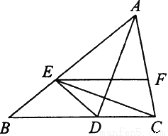
如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:解答题
平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(2,7) ,直线l经过A点且平行于x
轴,直线l上的动点C从A点出发以每秒4个单位的速度沿直线l运动.若在x轴上有两点D、E,
连接DB、OB,连接EC、OC,满足DB=OB,EC=OC,设点C运动时间t秒,
(1) 如图1,若动点C从A点出发向左运动,当t=1秒时,
①求线段BC的长和点E的坐标;
②求此时DE与AC的数量关系?
(2)探究:动点C在直线l运动,无论t取何值,是否都存在上述(1)②中的数量关系? 若存在,请证明;若不存在,请说明理由.
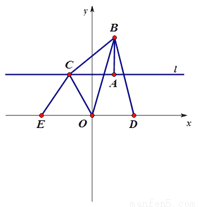
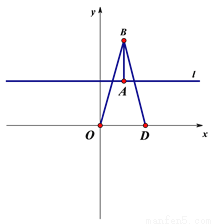
图1 图2
(1) ①BC=5, E(-4,0)②DE=2AC (2)存在,证明见解析 【解析】试题分析:(1)①根据题意可知AC=4,AB=3,由勾股定理即可得BC的长,再根据EC=OC以及点C的坐标即可得点E的坐标; ②由点B的坐标以及DB=OB即可得点D的坐标,从而得到DE的长,从而可得; (2)由题意可知AC=4t,C(2-4t,4),从而可得E(4-8t,0),由D(4,0)可得D...查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:填空题
如果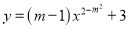 是一次函数,则
是一次函数,则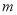 的值是________________.
的值是________________.
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
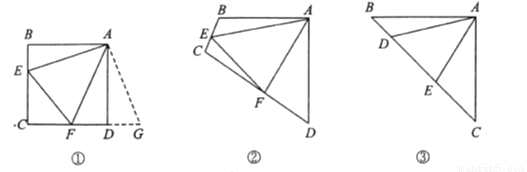
原题:如图①,点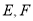 分别在正方形
分别在正方形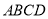 的边
的边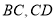 上,
上, 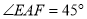 ,连接
,连接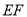 ,则
,则 ,试说明理由.
,试说明理由.
(1)思路梳理
因为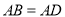 ,所以把
,所以把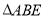 绕点
绕点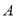 逆时针旋转90°至
逆时针旋转90°至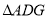 ,可使
,可使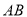 与
与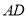 重合.因为
重合.因为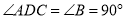 ,所以
,所以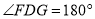 ,点
,点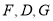 共线.
共线.
根据 ,易证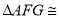 ,得
,得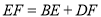 .请证明.
.请证明.
(2)类比引申
如图②,四边形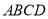 中,
中, 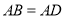 ,
, 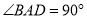 ,点
,点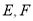 分别在边
分别在边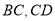 上,
上, 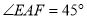 .若
.若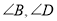 都不是直角,则当
都不是直角,则当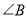 与
与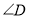 满足等量关系时,
满足等量关系时, 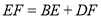 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在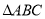 中,
中, 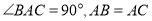 ,点
,点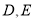 均在边
均在边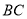 上,且
上,且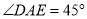 .猜想
.猜想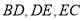 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:填空题
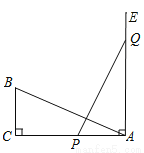
如图, 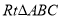 中,
中, 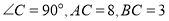 ,
, 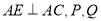 分别是
分别是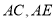 上动点,且
上动点,且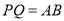 ,当
,当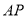 =_______时,才能使
=_______时,才能使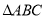 和
和 全等.
全等.
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:填空题
如果等腰三角形的底角是50°,那么这个三角形的顶角的度数是___________
80° 【解析】试题解析:180°-50°×2 =180°-100° =80°. 故这个三角形的顶角的度数是80°.查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:填空题
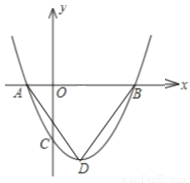
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D, 其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,当a=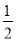 时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
查看答案和解析>>
科目:初中数学 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:单选题
方程x(x-2)+x-2=0的解是( )
A. 2 B. -2,1 C. -1 D. 2,-1
D 【解析】试题分析:x(x-2)+x-2=0, (x-2)(x+1)=0, ∴x-2=0或x+1=0, ∴x1=2,x2=-1. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com