练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

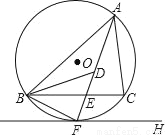
    如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连接AF交BC于E，∠ABC的平分线BD交AF于D，连接BF．

    （1）证明：AF平分∠BAC；

    （2）证明：BF=FD；

    （3）若EF=4，DE=3，求AD的长．

    （1）证明见解析；（2）证明见解析；（3）. 【解析】试题分析：（1）连接OF，通过切线的性质证OF⊥FH，进而由FH∥BC，得OF⊥BC，即可由垂径定理得到F是弧BC的中点，根据圆周角定理可得∠BAF=∠CAF，由此得证； （2）求BF=FD，可证两边的对角相等；易知∠DBF=∠DBC+∠FBC，∠BDF=∠BAD+∠ABD；观察上述两个式子，∠ABD、∠CBD是被角平分线平分∠AB...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型：单选题

    如果关于x的方程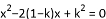有实数根α、β，那么α+β的取值范围是( )

    A. α+β≥1 B. α＋β≤1 C. α＋β≥ D. α＋β≤

    A 【解析】试题解析：∵a=1，b=-2（1-k），c=k2， ∴△=b2-4ac=[-2（1-k）]2-4×1×k2≥0， ∴k≤， ∵a+β=2（1-k）=2-2k， 而k≤， ∴α+β≥1． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：解答题

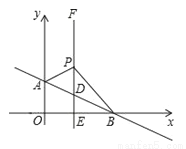
    如图，平面直角坐标系中，直线AB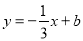： 交y轴于点A（0，1），交x轴于点B．过点E（1，0）作x轴的垂线EF交AB于点D，P是直线EF上一动点，且在点D的上方，设P（1，n）．

    （1）直线AB的表达式为______；

    （2）求△ABP的面积（用含n的代数式表示）；

    （3）当S△ABP=2时，以PB为边在第一象限作等腰直角三角形BPC，直接写出点C的坐标．

    （1）；（2）S△PAB=n﹣1；（3）C（3，4）或（5，2）或（3，2）． 【解析】试题分析：（1）把A的坐标代入直线AB的解析式，即可求得b的值，然后在解析式中，令y=0，求得x的值，即可求得B的坐标； （2）过点A作AM⊥PD，垂足为M，求得AM的长，即可求得△BPD和△PAB的面积，二者的和即可求得； （3）当S△ABP=2时， n﹣1=2，解得n=2，则∠OBP=45...

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：填空题

    将一次函数y=2x的图象向上平移1个单位，所得图象对应的函数表达式为__________．

    y=2x+1． 【解析】由“上加下减”的原则可知，将函数y=2x的图象向上平移1个单位所得函数的解析式为y=2x+1， 故答案为：y=2x+1．

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：单选题

    若点（3，m）在函数y= 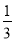x+2的图象上．则m的值为（　　）

    A. 0 B. 1 C. 2 D. 3

    D 【解析】点(3，m)在函数y= x+2有m=,m=1,所以选B.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省中考数学模拟试卷 题型：解答题

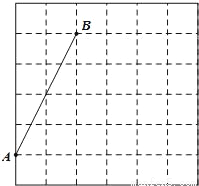
    如图，在每个小正方形的边长均为1的方格纸中，有线段AB，点A、B均在小正方形的顶点上．

    （1）在方格纸中画出以AB为一边的等腰△ABC，点C在小正方形的顶点上，且△ABC的面积为6．

    （2）在方格纸中画出△ABC的中线BD，并把线段BD绕点C逆时针旋转90°，画出旋转后的线段EF（B与E对应，D与F对应），连接BF，请直接写出BF的长．

    (1)作图见解析；（2）5. 【解析】试题分析：(1)根据等腰三角形的性质画出图形即可；(2)根据图形旋转的性质画出线段EF，再根据勾股定理求得BF的长即可. 试题解析： （1）如图所示，△ABC为所求三角形； （2）如图所示，EF为所求的线段，BF=5．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省中考数学模拟试卷 题型：填空题

    已知x2+3x+5的值为11，则代数式3x2+9x+12的值为_____．

    30 【解析】试题解析：∵x2+3x+5=11， ∴x2+3x=6， ∴原式=3（x2+3x）+12 =3×6+12 =30．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年上学期苏州市初三数学期末综合检测 题型：解答题

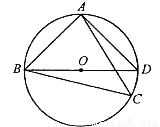
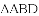
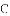
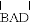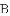
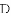
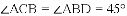
    如图，为的外接圆上的一动点(点不在上，且不与点、重合)，.

    (1)求证: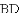是该外接圆的直径;

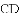
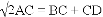    (2)连接，求证:涯;

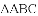
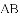
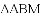
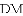
    (3)若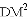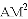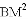关于直线的对称图形为，连接，试探究、、三者之间满足的等量关系，并证明你的结论.

    见解析 【解析】试题分析：（1）要证明BD是该外接圆的直径，只需要证明∠BAD是直角即可，又因为∠ABD=45°，所以需要证明∠ADB=45°； （2）在CD延长线上截取DE=BC，连接EA，只需要证明△EAF是等腰直角三角形即可得出结论； （3）过点M作MF⊥MB于点M，过点A作AF⊥MA于点A，MF与AF交于点F，证明△AMF是等腰三角形后，可得出AM=AF，MF=AM，然后...

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期中数学试卷 题型：单选题

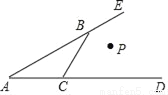
    如图，已知点P到AE，AD，BC的距离相等，有下列说法：

    ①点P在∠BAC的平分线上；

    ②点P在∠CBE的平分线上；

    ③点P在∠BCD的平分线上；

    ④点P在∠BAC，∠CBE，∠BCD的平分线的交点上．

    其中正确的是（　　）

    A. ①②③④ B. ①②③ C. ④ D. ②③

    A 【解析】试题分析： 根据在角的内部到角的两边距离相等的点在角的平分线上．∵点P到AE、AD、BC的距离相等，∴点P在∠BAC的平分线上，故①正确；点P在∠CBE的平分线上，故②正确；点P在∠BCD的平分线上，故③正确； 点P在∠BAC，∠CBE，∠BCD的平分线的交点上，故④正确，综上所述，正确的是①②③④．故选A．

    查看答案和解析>>

    同步练习册答案