
如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是( )
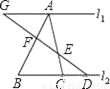
A. 5:2 B. 4:1 C. 2:1 D. 3:2
C 【解析】试题解析:∵AF:FB=2:3,BC:CD=2:1 ∴设AF=2x,BF=3x,BC=2y,CD=y 在△AGF和△BDF中, ∴ ∴AG=2y 在△AGE和△CDE中,AE:EC=AG:CD=2y:y=2:1 故选C. 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:3x(x﹣2)=2(x﹣2).(因式分解法)
x1=2,x2=. 【解析】移项,得3x(x﹣2)﹣2(x﹣2)=0, 分解因式,得(x﹣2)(3x﹣2)=0, x-2=0,3x-2=0, 解得x1=2,x2=查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:填空题
将一次函数y=2x的图象向上平移1个单位,所得图象对应的函数表达式为__________.
y=2x+1. 【解析】由“上加下减”的原则可知,将函数y=2x的图象向上平移1个单位所得函数的解析式为y=2x+1, 故答案为:y=2x+1.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
(1)在方格纸中画出以AB为一边的等腰△ABC,点C在小正方形的顶点上,且△ABC的面积为6.
(2)在方格纸中画出△ABC的中线BD,并把线段BD绕点C逆时针旋转90°,画出旋转后的线段EF(B与E对应,D与F对应),连接BF,请直接写出BF的长.
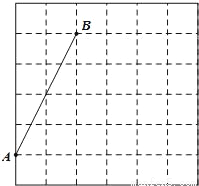
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:填空题
已知x2+3x+5的值为11,则代数式3x2+9x+12的值为_____.
30 【解析】试题解析:∵x2+3x+5=11, ∴x2+3x=6, ∴原式=3(x2+3x)+12 =3×6+12 =30.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:单选题
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 的中点,则下列结论不成立的是( )
的中点,则下列结论不成立的是( )
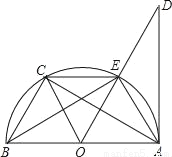
A. OC∥AE B. EC=BC C. ∠DAE=∠ABE D. AC⊥OE
D 【解析】试题分析:由C为弧的中点,利用垂径定理的逆定理得出OC垂直于BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE垂直于BE,即可确定出OC与AE平行,选项A正确; 由C为弧BE中点,即=,利用等弧对等弦,得到BC=EC,选项B正确; 由AD为圆的切线,得到AD垂直于OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等得到∠DAE=∠A...查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,
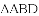
 上,且不与点
上,且不与点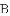
(1)求证: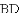
(2)连接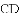
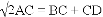 ;
;
(3)若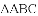
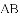
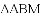
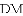
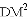 、
、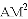 、
、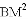 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:单选题
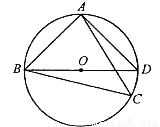
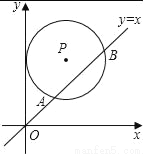
如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
,则a的值是( )
A. 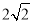 B. 2+
B. 2+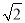 C.
C. 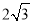 D.
D. 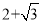
查看答案和解析>>
科目:初中数学 来源:安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
一辆慢车从甲地匀速行使至乙地,一辆快车同时从乙地匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(h)的对应关系如图所示,当两车相距300km时,x为________h.
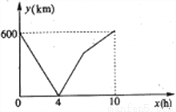
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com