练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

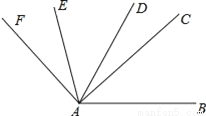
    如图，已知∠BAE=∠CAF=110°，∠CAE=60°，AD是∠BAF的角平分线，求∠BAD的度数．

    80°． 【解析】试题分析： 由∠BAE=110°，∠CAE=60°，可得∠BAC=110°﹣60°=50°，结合∠CAF=110°，可得∠BAF=110°+50°=160°，再由AD平分∠BAF即可得∠BAD=80°. 试题解析： ∵∠BAE=110°，∠CAE=60°， ∴∠BAC=110°﹣60°=50°， 又∵∠CAF=110°， ∴∠BAF=11...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷（C卷） 题型：填空题

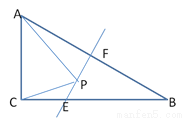
    如图，Rt△ABC中，∠C=Rt∠，AC=3，BC=4，AB=5，EF垂直平分AB，点P为直线EF上一动点，则 △APC周长的最小值为____

    7． 【解析】由EF垂直平分AB，可知点A与点B关于直线EF对称，所以当点P与点E重合时，∆APC周长的最小， 连接AE，∵EF垂直平分AB，∴AE=BE， ∴AE+CE+AC=BE+CE+AC=BC+AC=4+3=7， 即△APC周长的最小值为7， 故答案为：7.

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 小题易丢分 题型：单选题

    （2015临沂）在平面直角坐标系中，直线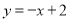与反比例函数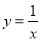的图象有唯一公共点，若直线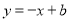与反比例函数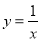的图象有2个公共点，则b的取值范围是（　　）

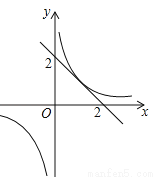
    A. b＞2 B. ﹣2＜b＜2 C. b＞2或b＜﹣2 D. b＜﹣2

    C 【解析】试题分析：根据题意可知这个一次函数y =－x＋2和反比例函数的交点为（1，1），直线y =－x＋2与y轴的交点为（0，2），根据对称性可知直线y =－x＋2向下平移，得到y=-x+b，会与双曲线的另一支也有一个交点（-1，-1），且这时的直线y=-x+b与y轴的交点为（0，-2），即直线为y=-x-2，因此这两条直线与双曲线有两个交点时，直线y =－x＋2向上移，b的取值范围为值...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年八年级（上）期中数学试卷 题型：单选题

    如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（　　）

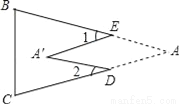
    A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2 C. 3∠A=2∠1+∠2 D. 3∠A=2（∠1+∠2）

    B 【解析】试题分析：利用三角形的内角和及平角的定义进行求解. 【解析】 设， ， 则， ∵， ， ∴， ， ， ∴. 2∠A=∠1+∠2. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年八年级（上）期中数学试卷 题型：单选题

    若下列各组值代表线段的长度，以它们为边能构成三角形的是（　　）

    A. 6、13、7 B. 6、6、12 C. 6、10、3 D. 6、9、13

    D 【解析】根据三角形任意两边之和大于第三边，得D正确.

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年七年级（上）期中数学试卷（解析版） 题型：解答题

    按要求作图：如图，在同一平面内有四个点A、B、C、D．

    （1）画射线CD；

    （2）画直线AD；

    （3）连接AB；

    （4）直线BD与直线AC相交于点O；

    （5）请说明AD+AB＞BD的理由．

    见解析 【解析】试题分析： （1）至（4）小题按题目中的要求规范的画出相应图形即可； （5）根据“两点之间，线段最短”即可得到：AD+AB>BD. 试题解析： 按（1）、（2）、（3）、（4）中的要求画图如下： （5）∵两点之间线段最短， ∴AD+AB＞BD．

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年七年级（上）期中数学试卷（解析版） 题型：单选题

    一个长方形的周长是40，若长方形的一边用字母x表示，则长方形的面积是（　　）

    A. x（20﹣x） B. x（40﹣x） C. x（40﹣2x） D. x（20+x）

    A 【解析】∵长方形的周长为40，一边长为， ∴与长为的边相邻的另一边长为， ∴长方形的面积= . 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省韶关市南雄市中考数学模拟试卷 题型：填空题

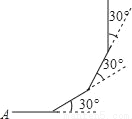
    如图：小亮从A点出发，沿直线前进10米后向左转30度，再沿直线前进10米，又向左转30度，??照这样走下去，他第一次回到出发点A点时，一共走了______米？

    120 【解析】试题分析：由题意可知小亮所走的路线为一个正多边形，根据多边形的外角和即可求出答案． 【解析】 ∵360÷30=12， ∴他需要走12次才会回到原来的起点，即一共走了12×10=120米． 故答案为：120．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：解答题

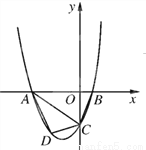
    已知，如图抛物线y＝ax2＋3ax＋c(a>0)与y轴交于点C，与x轴交于A， B两点，点A在点B左侧．点B的坐标为(1,0)，OC＝3OB.

    （1）求抛物线的解析式；

    （2）若点D是线段AC下方抛物线上的动点，过点D做x轴的垂线，交AC于点E,求线段DE的最大值.

    （3）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值.

    （1）y＝x2＋x－3；（2）3；（3）四边形ABCD面积有最大值. 【解析】试题分析：（1）已知了B点坐标，易求得OB、OC的长，进而可将B、C的坐标代入抛物线中，求出待定系数的值，即可得出抛物线的解析式． （2）根据A、C的坐标，易求得直线AC的解析式．可过D作x轴的垂线，交AC于E，x轴于F；易得△ADC的面积是DE与OA积的一半，可设出F点的坐标，分别代入直线AC和抛物线的解析...

    查看答案和解析>>

    同步练习册答案