
已知二次函数的图象开口向下,且其图象顶点位于第一象限内,请写出一个满足上述条件的二次函数解析式为_____(表示为y=a(x+m)2+k的形式).
y=﹣(x﹣1)2+1(答案不唯一) 【解析】因为二次函数的顶点坐标为:(-m,k),根据题意图象的顶点位于第一象限,所以可得:m<0,k>0,因此满足m<0,k>0的点即可,故答案为: (答案不唯一). 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:单选题
下列变形正确的是( ).
A. 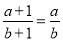 B.
B. 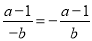 C.
C. 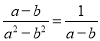 D.
D. 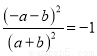
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
计算: 
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:解答题
如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).
(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;
(2)当△ABE与△BCE相似时,求线段CD的长;
(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.

查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
如图,平面上七个点A、B、C、D、E、F、G,图中所有的连线长均相等,则cos∠BAF=_____.
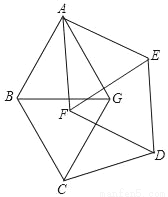
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC=_____.
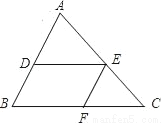
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:单选题
已知二次函数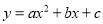 的图像大致如图所示,则下列关系式中成立的是( )
的图像大致如图所示,则下列关系式中成立的是( )
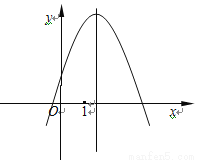
A. 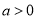 B.
B. 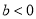 C.
C. 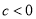 D.
D. 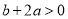 .
.
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
如果多项式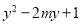 是完全平方式,那么
是完全平方式,那么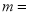 ________
________
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:单选题
下列有理式中①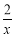 ,②
,②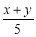 ,③
,③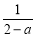 ,④
,④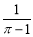 中分式有( )个.
中分式有( )个.
A、1个 B、 2个 C、3个 D、4个
B. 【解析】 试题分析:根据分式的定义,分母中含有字母的式子有①,③,所以其中的分式有两个. 故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com