
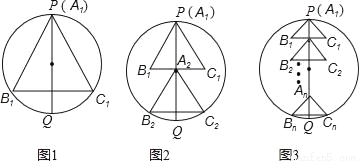
��ͼ����֪��O�İ뾶Ϊ1��PQ�ǡ�O��ֱ����n����ͬ������������PQ�ų�һ�У������������ζ�����PQ�Գƣ����е�һ����A1B1C1�Ķ���A1���P�غϣ��ڶ�����A2B2C2�Ķ���A2��B1C1��PQ�Ľ��㣬�������һ����AnBnCn�Ķ���Bn��Cn��Բ�ϣ���ͼ1����n=1ʱ���������εı߳�a1=_____����ͼ2����n=2ʱ���������εı߳�a2=_____����ͼ3���������εı߳�an=_____���ú�n�Ĵ���ʽ��ʾ����
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㶫ʡ�����н�������У2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
���䷽���ⷽ��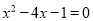 ���䷽��õ��ķ���Ϊ�� ��
���䷽��õ��ķ���Ϊ�� ��
A. 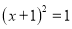 B.
B. 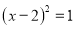 C.
C. 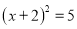 D.
D. 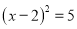
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������˳����2018�������ѧ����ĩ������ѧ�Ծ� ���ͣ������
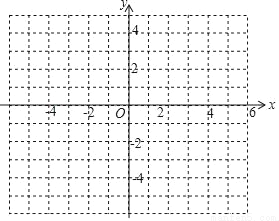
��ƽ��ֱ������ϵxOy�У�������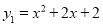 ���Կ�����������
���Կ�����������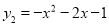 �������ɴ�ͼ�εı仯��ƽ�ơ����ۡ���ת���õ��ģ�д��һ����������y2�õ�������y1�Ĺ��̣�__________��
�������ɴ�ͼ�εı仯��ƽ�ơ����ۡ���ת���õ��ģ�д��һ����������y2�õ�������y1�Ĺ��̣�__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���������о��꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
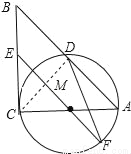
��ͼ����Rt��ABC�У���C=90�㣬��ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ ��ED=2���ӳ�EO����O��F������DF��AF�����ADF�������
��ED=2���ӳ�EO����O��F������DF��AF�����ADF�������
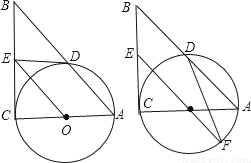
���𰸡���1��֤������������2��
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��
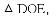
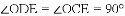
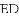
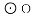
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�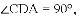
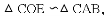
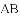
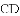
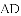
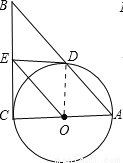
���������(1)֤��������OD��
��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
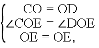 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
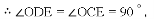
��ED��OD��
��ED��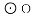
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
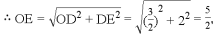
��OE��AB��
���COE�ס�CAB��
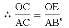 ��AB=5��
��AB=5��
��AC��ֱ����
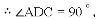
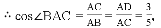
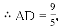
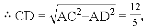
��EF��AB��
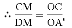
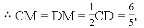
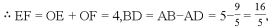
��S��ADF=S����ABEF?S����DBEF
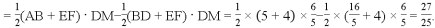
���ADF�����Ϊ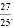
�����͡������
��������
25
��֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN�����DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���������о��꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
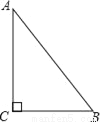
��Rt��ABC�У���C=90�㣮
��1���ó߹���ͼ��Rt��ABC������P����������ͼ�ۼ�����Ҫ��д������֤������
��2������ΪֻҪ֪��Rt��ABC��һ���ߵij����������������������֮��ľ��룿������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���������о��꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ���ѡ��
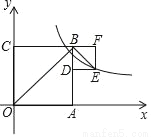
��ͼ�������߳��ֱ�Ϊa��b��a��b��������������һ������C��B��F��ͬһֱ���ϣ�����������y= �ڵ�һ����ͼ��С���������¶���E����OB2��BE2=10����k��ֵ�ǣ�������
�ڵ�һ����ͼ��С���������¶���E����OB2��BE2=10����k��ֵ�ǣ�������
A. 3 B. 4 C. 5 D. 4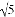
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���������о��꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ���ѡ��
-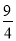 �ͣ�-
�ͣ�-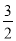 ��2�Ĺ�ϵ�ǣ� ��
��2�Ĺ�ϵ�ǣ� ��
A. ��� B. ��Ϊ�෴�� C. ��Ϊ���� D. �����𰸶�����ȷ
B �����������ݳ˷���������ʣ���֪��-��2=�������ǻ�Ϊ�෴��. ��ѡ��B.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڰ��꼶��ѧ�����Ծ� ���ͣ������
����ʽx2��8x+k��һ����ȫƽ��ʽ����k=_____��
16 ��������k=����4��2=16. �ʴ�Ϊ16.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��һ����ֱ�Ĺ�·���� ��
�� ���أ��״�
���أ��״� ��ȥ
��ȥ �أ��Ҵ�
�أ��Ҵ� ��ȥ
��ȥ ��Ȼ������ԭ·����
��Ȼ������ԭ·���� �أ�����ʱ���ٶ���ԭ����2������ͼ�Ǽס���������
�أ�����ʱ���ٶ���ԭ����2������ͼ�Ǽס��������� �صľ���
�صľ��� ��ǧ�ף���ʱ��
��ǧ�ף���ʱ�� ��Сʱ��֮��ĺ���ͼ��
��Сʱ��֮��ĺ���ͼ��

�����ͼ��ش��������⣺
��1�� ��
�� ���صľ����� ǧ�ף�
���صľ����� ǧ�ף�  ��
��
��2���� �����꣬����������ʵ�����壻
�����꣬����������ʵ�����壻
��3����ֱ��д���� ȡ��ֵʱ�������������15ǧ�ף�
ȡ��ֵʱ�������������15ǧ�ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com