练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抛物线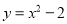的顶点坐标为（ ）

    A. （2，0） B. （-2，0） C. （0，2） D. （0，-2）

    D 【解析】试题分析：对于二次函数的顶点坐标为(0，b)，根据题意可知二次函数的顶点坐标为(0，-2)，故选择D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：解答题

    一份试卷，一共30道选择题，答对一题得3分，答错一题扣1分，小红每题都答了，共得78分，那么小红答对了几道题？请根据题意，列出方程．

    3x－（30－x）×1＝78． 【解析】等量关系为:答题得分=答对的题得分－答错题扣的分,设答对了x道题,则答错了(30－x)道题,答对题得分为:3x,答错的题扣分为: (30－x),根据题意可列出方程. 试题解析:设小红答对了x道题,由题意得: 3x－（30－x）×1＝78.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级数学上册 第23章 旋转 同步单元检测试卷（Word版附答案） 题型：填空题

    如图所示，已知抛物线C1，抛物线C2关于原点中心对称．如果抛物线C1的解析式为y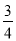＝ (x＋2)2－1，那么抛物线C2的解析式为____________________.

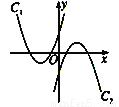
    y＝ (x－2)2＋1 【解析】试题分析：已知抛物线C1，抛物线C2关于原点中心对称．所以抛物线上所有的点也关于原点中心对称，根据抛物线C1的解析式y＝ (x＋2)2－1，可知顶点坐标是（-2，-1），对称轴是x=-2，两抛物线的形状，开口大小均相同，开口方向相反，所以二次项系数应互为相反数，根据C1的解析式，可以知道C2的二次项系数为，顶点坐标为（2,1）.对称轴是x=2，所以可以得到C2...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（3）测试 题型：解答题

    如图4所示，一座抛物线型拱桥，桥下水面宽度是4m，拱高是2m，当水面下降1m后，水面宽度是多少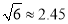？（，结果保留0.1m）

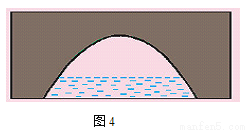
    4.9 【解析】试题分析：首先以水面的水平线为x轴，抛物线两端点中点为原点设立平面直角坐标系，设函数解析式为： ，将(0，2)和(2，0)代入求出函数解析式，最后将y=-1代入函数解析式求出x的值，从而的得出水面的宽度． 试题解析：设水面的水平线为x轴，抛物线两端点中点为原点设立平面直角坐标系， 设抛物线的函数关系式为： ， 因为抛物线过点（0，2）， 所以有， 又因为抛物...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（3）测试 题型：单选题

    图3是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯．若把拱桥的截面图放在平面直角坐标系中，则两盏景观灯之间的水平距离是（ ）

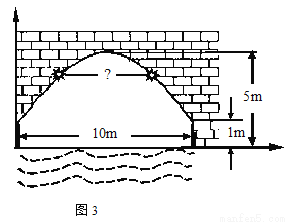
    A .3m B.4m C.5m D.6m

    C 【解析】试题分析：设距水面1m的水平线为x轴，抛物线两端点中点为原点设立平面直角坐标系， 则抛物线左端点为(-5，0)，右端点为(5，0)，顶点为(0，4)， 设抛物线为： ，将(5，0)代入可得函数解析式为： ； 将y=3代入函数解析式可得： ，则两盏景观灯之间的水平距离为5m，故选择C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型：解答题

    如图，郑某把一块边长为a m的正方形的土地租给李某种植，他对李某说：“我把你这块地的一边减少5 m，另一边增加5 m，继续租给你，你也没有吃亏，你看如何”.李某一听，觉得自己好像没有吃亏，就答应了.同学们，你们觉得李某有没有吃亏？请说明理由.

    【答案】李某吃亏了，理由见解析.

    【解析】试题分析：计算阴影部分面积和原正方形面积作比较.

    试题解析：

    【解析】
    李某吃亏了.理由如下：

    ∵（a+5）（a-5）=a2-25＜a2，

    ∴李某少种了25 m2地，李某吃亏了.

    【题型】解答题
    【结束】
    20

    计算：（1）992-102×98;

    （2）［x（x2y2-xy）-y（x2-x3y）］÷x2y.

    （1）-195（2）2xy-2 【解析】试题分析：（1）利用平方差公式，完全平方公式简便计算. (2)提取公因式，化简. 试题解析： （1）原式=（100-1）2-（100+2）×（100-2） =（1002-200+1）-（1002-4）=-200+5=-195. （2）原式=［x2y（xy-1）-x2y（1-xy）］÷x2y =2x2y（xy-1）÷x...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型：填空题

    若m2-n2=6，且m-n=3，则m+n =_______________

    【答案】2

    【解析】解析：∵m2-n2=（m+n）（m-n）=3（m+n）=6，

    ∴m+n=2.

    【题型】填空题
    【结束】
    13

    如果4x2+ax+9是一个完全平方式，那么a的值为______.

    ±12 【解析】解析：∵（2x±3）2=4x2±12x+9=4x2+ax+9， ∴a=±12.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.3二次函数ya（x-h）2+k的图象和性质（3）测试 题型：填空题

    抛物线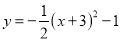有最______点，其坐标是______．当x＝______时，y的最______值是______；当x______时，y随x增大而增大．

    高 (－3，－1) －3 大 －1 ≤－3． 【解析】【解析】 抛物线有最高点，其坐标是（－3，－1）．当x＝－3时，y的最大值是－1；当x≤－3时，y随x增大而增大． 故答案为：高；（－3，－1） ；－3 ； 大；－1 ； ≤－3．

    查看答案和解析>>

    科目：初中数学 来源：2017年秋四川泸县第四中学九年级第二次阶段性考试数学试卷 题型：解答题

    菜农李大伯种植的某蔬菜计划以每千克5元的单价对外批发销售，由于部分菜农盲目扩大种植，造成该蔬菜滞销．李大伯为了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元的单价对外批发销售．

    （1）求平均每次下调的百分率；

    （2）小华准备到李大伯处购买5吨该蔬菜，因数量多，李大伯决定再给予两种优惠方案以供选择：方案一：打九折销售；方案二：不打折，每吨优惠现金200元．

    试问小华选择哪种方案更优惠，请说明理由．

    （1）平均每次下调的百分率是20%.（2）小华选择方案一购买更优惠. 【解析】试题分析：（1）设出平均每次下调的百分率，根据从5元下调到3.2列出一元二次方程求解即可； （2）根据优惠方案分别求得两种方案的费用后比较即可得到结果． 试题解析：（1）设平均每次下调的百分率为x． 由题意，得5（1﹣x）2=3.2． 解这个方程，得x1=0.2，x2=1.8（不符合题意），...

    查看答案和解析>>

    同步练习册答案