
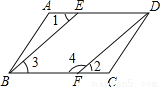
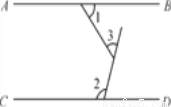
如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请完善说明过程,并在括号内填上相应依据.
【解析】
∵AD∥BC ( ) ,
∴∠1=∠3 ( ),
∵∠1=∠2(已知),
∴∠2=∠3 ( ),
∴____∥____ ( ),
∴∠3+∠4=180°( ) .
答案见解析 【解析】试题分析:根据平行线的性质推出∠1=∠3=∠2,根据平行线的判定推出BE∥DF,根据平行线的性质推出即可. 试题解析:∵AD∥BC(已知), ∴∠1=∠3(两直线平行,内错角相等), ∵∠1=∠2, ∴∠2=∠3(等量代换), ∴BE∥DF(同位角相等,两直线平行), ∴∠3+∠4=180°(两直线平行,同旁内角互补).科目:初中数学 来源:2017-2018学年七年级数学人教版上册:全册综合测试卷 题型:单选题
-(-3)的绝对值是( )
A. -3 B. 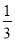 C. -
C. -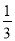 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:单选题
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( )
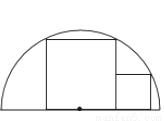
A. (4+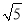 )cm B. 9cm C. 4
)cm B. 9cm C. 4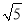 cm D. 6
cm D. 6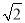 cm
cm
查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2017-2018学年七年级上学期期末质量检测数学试卷 题型:填空题
黄山主峰一天早晨气温为﹣1℃,中午上升了8℃,夜间又下降了10℃,那么这天夜间黄山主峰的气温是_______________
-3℃ 【解析】试题分析:因为泰山主峰一天早晨气温为-1℃,中午上升了8℃,夜间又下降了10℃,所以这天夜间泰山主峰的气温是-1+8-10=-3.查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2017-2018学年七年级上学期期末质量检测数学试卷 题型:单选题
下列各图中所给的线段、射线、直线能相交的是( )
A. 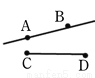 B.
B. 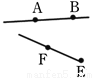 C.
C. 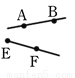 D.
D. 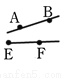
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第五章《平行线的性质与判定》同步练习(含答案) 题型:填空题
如图,AB∥CD,∠1=50°,∠2=110°,则∠3=____________.
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第五章《平行线的性质与判定》同步练习(含答案) 题型:单选题
若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A. 70° B. 86° C. 70°或86° D. 30°或38°
D 【解析】试题解析:∵∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x-20)°, ∴(2x+10)+(3x-20)=180,2x+10=3x-20, x=38,x=30, 当x=38时,∠α=86°, 当x=30时,∠α=70°, 故选C.查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市东城区七年级(上)期末数学试卷 题型:填空题
计算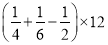 =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第五章《相交线与平行线--垂线》同步练习 题型:解答题
如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
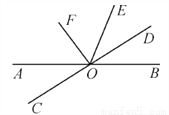
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
(1) OF⊥OD,理由见解析;(2) 60°. 【解析】试题分析:(1)根据角平分线的性质,可得与的关系,根据角的和差,可得的度数,可得答案; (2)根据补角的性质, 可得的度数,根据角的和差,可得的度数,根据角平分线的性质,可得答案. 试题解析: (1)因为OF平分∠AOE, 所以∠AOF=∠EOF=∠AOE. 又因为∠DOE=∠BOD=∠BOE, 所以∠...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com