练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    利用加减消元法解方程组，下列做法正确的是(　 　)

    A. 要消去z，先将①＋②，再将①×2＋③ B. 要消去z，先将①＋②，再将①×3－③

    C. 要消去y，先将①－③×2，再将②－③ D. 要消去y，先将①－②×2，再将②＋③

    A 【解析】【解析】 利用加减消元法解方程组，要消去z，先将①+②，再将①×2+③，要消去y，先将①+②×2，再将②+③．故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省自贡市2017-2018学年上学期期末考试八年级数学试卷 题型：单选题

    如果把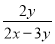中的x和y都扩大5倍，那么分式的值（ ）

    A. 不变 B. 扩大5倍 C. 缩小5倍 D. 扩大4倍

    A 【解析】试题解析： 分式的值不变. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（人教版）：期末检测题(二) 题型：单选题

    (2017·辽宁)如图，在?ABCD中，∠BAD＝120°，连接BD，作AE∥BD交CD的延长线于点E，过点E作EF⊥BC交BC的延长线于点F，若CF＝1，则AB的长是( )

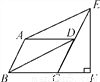
    A. 2 B. 1 C. 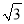D.

    B 【解析】∵四边形ABCD是平行四边形， ∴AB∥CD，AB=CD，∠BCD=∠BAD=120°， ∴∠ECF=180°-120°=60°， ∵AE∥BD， ∴四边形ABDE是平行四边形， ∴AB=DE， ∴AB=CE， ∵EF⊥BC， ∴∠EFC=90°， ∴∠CEF=30°， ∴EC=2CF=2， ∴AB=1. 故...

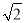
    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（华师大版）：期末检测2 题型：填空题

    AB∥CD，BC与AD相交于点M，N是射线CD上一点．若∠B＝65°，∠MDN＝135°，则∠AMB＝_______．

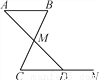
    70° 【解析】试题分析：∵AB∥CD， ∴∠A+∠MDN=180°， ∴∠A=180°﹣∠MDN=45°， 在△ABM中，∠AMB=180°﹣∠A﹣∠B=70°． 故答案为：70°．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（华师大版）：期末检测2 题型：单选题

    如图，△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H.下列结论：①∠DBE＝∠F；②2∠BEF＝∠BAF＋∠C；③∠F＝∠BAC－∠C；④∠BGH＝∠ABE＋∠C.其中正确的有(　 　)

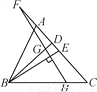
    A. ①②③ B. ①②④ C. ②③④ D. ①③④

    B 【解析】【解析】 ①∵BD⊥FD，∴∠FGD+∠F=90°，∵FH⊥BE，∴∠BGH+∠DBE=90°，∵∠FGD=∠BGH，∴∠DBE=∠F，①正确； ②∵BE平分∠ABC，∴∠ABE=∠CBE，∠BEF=∠CBE+∠C，∴2∠BEF=∠ABC+2∠C，∠BAF=∠ABC+∠C，∴2∠BEF=∠BAF+∠C，②正确； ③∠ABD=90°﹣∠BAC，∠DBE=∠ABE﹣∠A...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：解答题

    如图，一次函数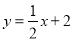分别交y轴、x轴于A、B两点，抛物线y=﹣x2+bx+c过A、B两点．

    （1）求这个抛物线的解析式；

    （2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？

    （3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．

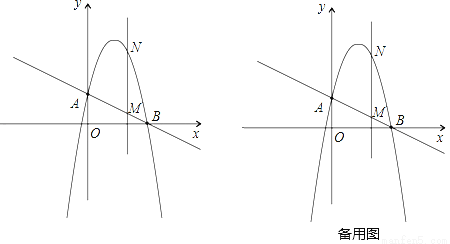
    （1）y=?x²+x+2；（2）t=2时，MN有最大值4;（3）(0,6),(0,?2)或(4,4)． 【解析】试题分析： （1）先由直线分别交y轴、x轴于点A、B这一条件求出点A、B的坐标，将所求坐标代入抛物线列出关于的值即可得到所求抛物线的解析式； （2）如图1，由题意可知点M的横坐标为t，根据点M在直线上，点N在（1）中所求抛物线上，可用含“t”的代数式表达出点M、N的坐标...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：解答题

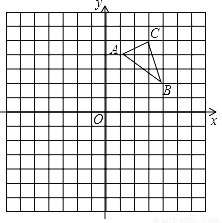
    如图所示，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）

    （1）请画出△A1B1C1，使△A1B1C1与△ABC关于原点对称；

    （2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出线段OB旋转到OB2扫过图形的面积．

    (1)见解析；（2）见解析， 【解析】试题分析： （1）连接AO并延长至A1，使A1O=AO得到点A1，同法作出点B1、C1，顺次连接所得三点，即可得到所求三角形； （2）过点O在AO的左侧作A2O⊥AO，使A2O=AO得到点A2，同法作出点B2、C2，顺次连接三点，即可得到所求三角形；由题意可知旋转过程中线段OB扫过的图形的面积就是扇形B2OB的面积，由题意可知∠B2OB=90...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：单选题

    已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（　　）

    A. 相交 B. 相切 C. 相离 D. 不能确定

    A 【解析】∵O的半径为3，圆心O到直线L的距离为2， ∵3>2，即：d

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年福建省龙岩市上杭县城区片三校七年级（上）联考数学试卷 题型：填空题

    比较大小： _____ ．（填“＞”或“＜”号）．

    ＞ 【解析】∵ ， ， ∴， 故答案为：>.

    查看答案和解析>>

    同步练习册答案