练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算72°34′÷2＋18°33′×4＝_____．

    110°29′ 【解析】【解析】 72°34′÷2＋18°33′×4=36°17′+72°132′=108°149′=110°29′．故答案为：110°29′．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省2017-2018学年七年级（上）期末模拟数学试卷 题型：单选题

    根据2010～2014年杭州市实现地区生产总值（简称GDP，单位：亿元）统计图所提供的信息，下列判断正确的是（　　）

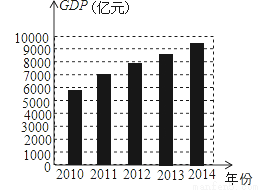
    A. 2012～2014年杭州市每年GDP增长率相同 B. 2014年杭州市的GDP比2010年翻一番

    C. 2010年杭州市的GDP未达到5400亿元 D. 2010～2014年杭州市的GDP逐年增长

    D 【解析】A、每年的增长量逐渐减小，所以每年GDP增长率不相同，所以A选项错误； B、2014年的GDP没有2010年的2倍，所以B选项错误； C、2010年杭州市的GDP超过到5400亿元，所以C选项错误； D、2010～2014年杭州市的GDP逐年增长，所以D选项正确． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2015-2016学年七年级上学期期末考试数学试卷 题型：填空题

    计算： =___________．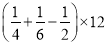

    －1 【解析】原式=×12+×12-×12=3+2-6=-1. 故答案为：-1.

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    如图，已知线段AB和CD的公共部分BD=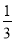AB= 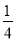CD，线段AB、CD的中点E，F之间距离是10cm，求AB，CD的长．

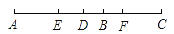
    AB=12cm，CD=16cm． 【解析】试题分析：先设BD=xcm，由题意得AB=3xcm，CD=4xcm，AC=6xcm，再根据中点的定义，用含x的式子表示出AE=1.5xcm和CF=2xcm，再根据EF=AC-AE-CF=2.5xcm，且E、F之间距离是EF=10cm，所以2.5x=10，解方程求得x的值，即可求AB，CD的长． 试题解析：【解析】 设BD=xcm，则AB=3x...

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型：填空题

    一列数：1，－3，9，－27，81，－243，…，其中某三个相邻数的和是－1701，则这三个数中最大的数是_____．

    729 【解析】设最小的数为（-3）n， 则（-3）n+（-3）n+1+（-3）n+2=-1701， 解得（-3）n=-243=（-3）5， 所以这三个数分别是（-3）5，（-3）6，（-3）7． 则这三个数中最大的数是（-3）6=729．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

    下列叙述不正确的是（　　）

    A. 若点C在线段BA的延长线上，则BA＝AC－BC

    B. 在平面内，两点之间，线段最短

    C. 若点C在线段AB上，则AB＝AC＋BC

    D. 若A、B、C三点在同一条直线上，则AB≤AC＋BC

    A 【解析】解：A．根据线段的延长线的概念，则BA=BC﹣AC，故错误； B．根据两点之间，线段最短，显然正确； C．根据线段的和的计算，正确； D．根据两点之间，线段最短，显然正确． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市2016-2017下学期初一期末数学试卷 题型：解答题

    小彬和小明每天早晨坚持跑步，小彬每秒跑4米，小明每秒跑6米．

    (1)如果他们站在百米跑道的两端同时相向起跑，那么几秒后两人相遇?

    (2)如果小明站在百米跑道的起点处，小彬站在他前面10米处，两人同时同向起跑，几秒后小明能追上小彬？

    (2)如果他们都站在四百米环形跑道的起点处，两人同时同向起跑，几分钟后他们再次相遇？

    （1）10秒后两人相遇；（2）5秒后小彬追上小明；（3）分钟后小彬追上小明． 【解析】试题分析：（1）此问利用行程中的相遇问题解答，两人所行路程和等于总路程； （2）（3）此问利用行程中的追及问题解答，两人所行路程差等于两人相距的路程．这两问利用最基本的数量关系：速度×时间=路程． 试题解析：【解析】 （1）设x秒后两人相遇，根据题意得：6x+4x=100， 解得x=10...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市2016-2017下学期初一期末数学试卷 题型：填空题

    如图，共有_________条线段.

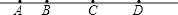
    6 【解析】【解析】 直线上有4个点，由两点确定一直线，线段有AB、AC、AD、BC、BD、CD共六条．故答案为：6．

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

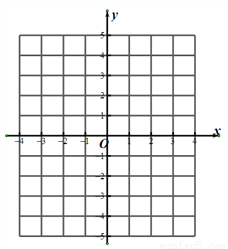
    平面直角坐标系中，△ABC的三个顶点坐标分别为A（0，4），B（2，4），C（3，－1）.

    （1）试在平面直角坐标系中，标出A、B、C三点；

    （2）求△ABC的面积.

    （3）若△A1B1C1与△ABC关于x轴对称，写出A1、B1、C1的坐标，并画出△A1B1C1。

    （1）画图见解析；（2）S△ABC=5；（3）A1（0，-4），B1（2，-4）C1（3，1） 【解析】试题分析：（1）根据三点的坐标，在直角坐标系中分别标出位置即可． （2）以AB为底，则点C到AB得距离即是底边AB的高，结合坐标系可得出高为点C的纵坐标的绝对值加上点B的纵坐标的绝对值，从而根据三角形的面积公式计算即可． （3）关于x轴对称的点的坐标，横坐标不变，纵坐标互为相反...

    查看答案和解析>>

    同步练习册答案