
阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
(1)an=(n为正整数);(2)是,是第11个三角形数;(3)T<2.理由参见解析. 【解析】 试题分析:(1)根据题意归纳总结得到一般性规律,写出即可;(2)66是三角形数,理由为:根据得出的规律确定出原因即可;(3)表示出T后,利用拆项法整理判断即可. 试题解析:(1)根据题意得:an=(n为正整数);(2)66是三角形数,理由如下:当=66时,解得:n=11或n=﹣12(... 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:福建省上杭县城区片2017-2018学年第一学期三校联考及答案 题型:填空题
轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3h,若船在静水中速度为26km/h,水流速度为2km/h,则A港和B港相距_____km.
504 【解析】试题分析:设轮船从A港顺流行驶到B港所需的时间为t,则从B港逆流返回A港的时间为t+3,因船速为26千米/小时,水速为2千米/时,则顺流速度为26+2=28km/h,逆流速度为26-2=24km/h,则有28t=24(t+3),解得t=18,所以A港和B港的距离为28×18=504km.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(七) 题型:解答题
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=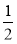 ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(七) 题型:单选题
半径为2的圆中,弦AB、AC的长分别2和2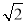 ,则∠BAC的度数是()
,则∠BAC的度数是()
A.15° B.105° C.15°或75° D.15°或105°
D. 【解析】 试题分析:分别作OD⊥AB,OE⊥AC,垂足分别是D、E. ∵OE⊥AC,OD⊥AB, ∴AE=AC=,AD=AB=1, ∴sin∠AOE=,sin∠AOD=, ∴∠AOE=45°,∠AOD=30°, ∴∠BAO=60°,∠CAO=90°-45°=45°, ∴∠BAC=45°+60°=105°,或∠BAC′=60°-45°=15°. ...查看答案和解析>>
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:解答题
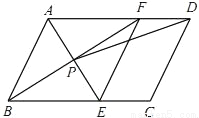
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:填空题
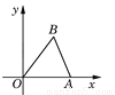
如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2∶1,放大得到△OA′B′,则顶点B的对应点B′的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:单选题
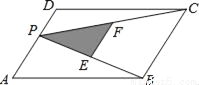
如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )
A. 4 B. 6 C. 8 D. 不能确定
C 【解析】试题分析:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB, ∴四边形PQCD与四边形APQB都为平行四边形, ∴△PDC≌△CQP,△ABP≌△QPB, ∴S△PDC=S△CQP,S△ABP=S△QPB, ∵EF为△PCB的中位线, ∴EF∥BC,EF=BC, ∴△PEF∽△PBC,且相似比为1:2, ∴S△PEF:S△PBC...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:填空题
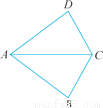
如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,则只需添加的一个条件可以是_________________________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:解答题
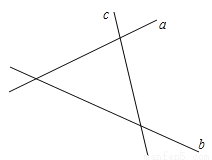
如图,有三条公路a,b,c,为了方便司机休息,路政部门确定修建一个休息站P,使它到三条公路的距离相等.(请用尺规作图,保留作图痕迹,不写作法.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com