
已知向量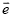 为单位向量,如果向量
为单位向量,如果向量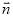 与向量
与向量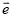 方向相反,且长度为3,那么向量
方向相反,且长度为3,那么向量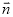 =________.(用单位向量
=________.(用单位向量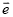 表示)
表示)
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:单选题
若将分式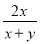 中的字母
中的字母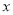 与
与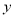 的值分别扩大为原来的10倍,则这个分式的值( )
的值分别扩大为原来的10倍,则这个分式的值( )
A. 扩大为原来的10倍 B. 扩大为原来的20倍 C. 不改变 D. 缩小为原来的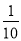 倍
倍
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
若关于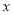 的方程
的方程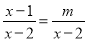 有增根,则
有增根,则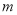 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:解答题
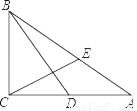
如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知抛物线y=ax2+bx+c开口向上,一条平行于x轴的直线截此抛物线于M、N两点,那么线段MN的长度随直线向上平移而变_____.(填“大”或“小”)
大 【解析】因为二次函数的开口向上,所以点M,N向上平移时,距离对称轴的距离越大,即MN的长度随直线向上平移而变大,故答案为:大.查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:单选题
如图,线段AB与CD交于点O,下列条件中能判定AC∥BD的是( )
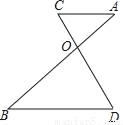
A. OC=1,OD=2,OA=3,OB=4 B. OA=1,AC=2,AB=3,BD=4
C. OC=1,OA=2,CD=3,OB=4 D. OC=1,OA=2,AB=3,CD=4.
C 【解析】根据平行线分线段成比例,因为,所以AC∥BD,故选C.查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
如图,在△ABC中,AD⊥BC于D, CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE AB;(2)AE=BE.
AB;(2)AE=BE.

查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
若分式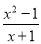 的值为0,则
的值为0,则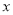 的值等于 .
的值等于 .
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
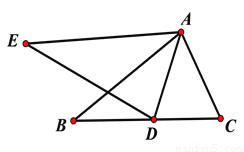
如图,△AED的顶点D在△ABC的BC边上,∠E=∠B,AE=AB, ∠EAB=∠DAC.
(1)求证:△AED≌△ABC.
(2)若∠E=40°,∠DAC=30°,求∠BAD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com