练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （ x2y2+y7+y5z）÷y2等于（ ）

    A. x2+ y5+y3z B. x2y2+y5z C. x2y +y5z D. x2y2+y7+y5z

    A 【解析】（ x2y2+y7+y5z）÷y2= x2y2÷y2+y7÷y2+y5z÷y2= x2+ y5+y3z, 故选：A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下册 第一章　整式的乘除 整式的运算 专题练习题 含答案 题型：解答题

    用简便方法计算：1002－992＋982－972＋…22－12

    5050 【解析】试题分析：分别将相邻的两个利用平方差公式进行简便计算，从而将原式转化为1到100的加法计算，从而得出答案． 试题解析：原式=(100+99)×(100-99)+(98+97)×(98-97)+…(2+1)×(2-1)=100+99+98+97+…2+1＝5050．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市张家港市2016-2017学年九年级（上）期末数学试卷 题型：填空题

    如图，MN是⊙O的直径，MN=2a，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，则 PA+PB的最小值为_____．（用含a的代数式表示）

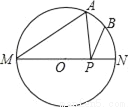
    a 【解析】作B点关于MN的对称点B′，连接AB′交MN于P，如图， 则PB=PB′， ∴PA+PB=PA+PB′=AB′， ∴此时PA+PB的值最小， ∵∠AMN=40°， ∴∠AON=80°， ∵点B为弧AN的中点， ∴∠BON=∠AON=40°， ∵B点关于MN的对称点B′， ∴∠B′ON=40°， ∴∠AOB′=120°， ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市张家港市2016-2017学年九年级（上）期末数学试卷 题型：单选题

    数据1，3，3，4，5的众数为（ ）

    A．1 B．3 C．4 D．5

    B． 【解析】 试题分析：3出现的次数最多，因而众数是3．故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型：填空题

    （-6a3-6a2c ）÷(-2a2)等于_______；

    3a+3c 【解析】（-6a3-6a2c ）÷(-2a2)= （-6a3) ÷ (-2a2)-6a2c÷(-2a2)= 3a+3c, 故答案为：3a+3c.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型：单选题

    （8x6y+8x3z）÷（2x）3等于（ ）

    A. x6y+x14z B. －x6y+x3yz C. x3y+z D. x6y+x3yz

    C 【解析】（8x6y+8x3z）÷（2x）3=（8x6y+8x3z）÷8x3=8x6y÷8x3+8x3z÷8x3= x3y+z, 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型：单选题

    -40a3b2÷（2a）3等于（ ）

    A. 20b B. -5b2 C. -a3b D. -20a2b

    B 【解析】-40a3b2÷（2a）3=-40a3b2÷8a3=-5b2， 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版5.1相交线同步练习 题型：解答题

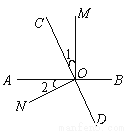
    如图,直线AB，CD相交于O点，OM⊥AB.

    （1）若∠1=∠2，求∠NOD；

    （2）若∠1=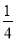∠BOC，求∠AOC与∠MOD.

    （1）90°；（2）∠AOC=60°，∠MOD＝150°. 【解析】（1）根据垂直的定义，可得∠AOC+∠1=90°由此易推出∠CON=90°，进而结合平角的定义即可解答本题； （2）根据垂直可知∠AOM=∠BOM=90°，结合∠1=∠BOC，可得∠1=30°，由此可以得到∠AOC与MOD的度数. 【解析】 （1）∵OM⊥AB， ∴∠AOM=90°，即∠AOC+∠1=90...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：填空题

    直线l同侧有A、B、C三点，若A、B两点确定的直线l1与B、C两点确定的直线l2都与l平行，则A、B、C三点_____，其理论依据是_____________.

    共线 过直线外一点，有且只有一条直线与已知直线平行 【解析】由题意可知∥∥L,且直线与直线都经过点B，所以根据平行公理“过直线外一点，有且只有一条直线与已知直线平行”可得A. B. C三点共线。 故答案为：共线，过直线外一点，有且只有一条直线与已知直线平行.

    查看答案和解析>>

    同步练习册答案