练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    综合题。

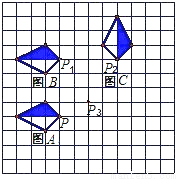
    （1）如图，在方格纸中先通过________，由图形A得到图形B，再由图形B先________（怎样平移），再________（怎样旋转）得到图形C（对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回答出旋转中心、旋转方向和旋转角度）；

    （2）如图，如果点P、P3的坐标分别为（0，0）、（2，1），写出点P2的坐标是________；

    （3）图形B能绕某点Q顺时针旋转90°得到图形C，则点Q的坐标是________；

    （4）图形A能绕某点R顺时针旋转90°得到图形C，则点R的坐标是________； 注：方格纸中的小正方形的边长为1个单位长度．

    （1）向上平移4个单位长；向右平移4个单位长度；绕点P2顺时针旋转90°；（2）（4，4）；（3）（2，2）；（4）（4，0）. 【解析】试题分析：（1）如图，根据方格纸中A和B的位置可以确定图形变换方式；然后根据B和C也可以确定图形变换方式； （2）根据（1）和已知条件首先确定P、P3和P2的关系，然后就可以确定P2的坐标； （3）由于图形B能绕某点Q顺时针旋转90°得到图形C...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：填空题

    x，y为实数，且满足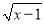+（3x+y﹣1）2=0，则=　 　．

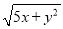    3. 【解析】已知+（3x+y﹣1）2=0，根据非负数的性质可得x﹣1=0，3x+y﹣1=0，解得x=1，y=﹣2，所以==3．

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：填空题

    若A（1，2），B（3，﹣3），C（x，y）三点可以确定一个圆，则x、y需要满足的条件是________

    5x+2y≠9 【解析】设直线AB的解析式为y=kx+b， ∵A（1，2），B（3，﹣3）， ∴ ，解得：k=，b=， ∴直线AB的解析式为y=x+， ∵点A（1，2），B（3，﹣3），C（x，y）三点可以确定一个圆时， ∴点C不在直线AB上， ∴5x+2y≠9， 故答案为：5x+2y≠9．

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：填空题

    △ABC中，若∠C-∠B=∠A，则△ABC的外角中最小的角是______（填“锐角”、“直角”或“钝角”）．

    直角 【解析】∵∠C?∠B=∠A， ∴∠C=∠A+∠B， ∵∠A+∠B+∠C=180°， ∴2∠C=180°， ∴∠C=90°， ∴△ABC的外角中最小的角是直角， 故答案为：直角.

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：单选题

    一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（　　）

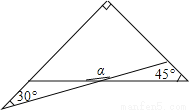
    A. 165° B. 120° C. 150° D. 135°

    A 【解析】利用直角三角形的性质求得∠2=60°；则由三角形外角的性质知∠2=∠1+45°=60°，所以易求∠1=15°；然后由邻补角的性质来求∠α的度数． 【解析】 如图， ∵∠2=90°-30°=60°，∴∠1=∠2-45°=15°，∴∠α=180°-∠1=165°．故选A．

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：解答题

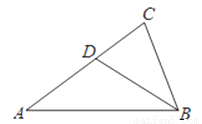
    如图，在△ABC中，D为AC边上一点，∠DBC=∠A．

    （1）求证：△ACD∽△ABC；

    （2）如果BC=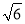， AC=3，求CD的长．

    （1）证明见解析；（2）CD=2. 【解析】试题分析：（1）根据相似三角形的判定得出即可； （2）根据相似得出比例式，代入求出即可． 试题解析：（1）∵∠DBC=∠A，∠C=∠C， ∴△ACD∽△ABC； （2）∵△ACD∽△ABC， ∴ ， ∴ ， ∴CD=2．

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：填空题

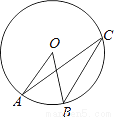
    如图，点O是⊙O的圆心，点A、B、C在⊙O上，AO∥BC，∠AOB=42°，则∠OAC的度数是________．

    21° 【解析】∵∠AOB=42°， ∴∠ACB=∠AOB=21°． ∵AO∥BC， ∴∠OAC=∠ACB=21°． 故答案为：21°．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：解答题

    如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=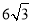，DE=3．

    求：

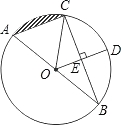
    （1）⊙O的半径；

    （2）弦AC的长；

    （3）阴影部分的面积．

    （1）6；（2）6；（3）6π-9． 【解析】 试题分析：（1）半径OD⊥BC，所以由垂径定理知：CE=BE，在直角△OCE中，根据勾股定理就可以求出OC的值； （2）根据AB是⊙O的直径，得到∠ACB=90°，因而在直角三角形ABC中根据勾股定理得到AC的长； （3）阴影部分的面积就是扇形OCA的面积减去△OAC的面积． 试题解析：（1）∵半径OD⊥BC， ∴...

    查看答案和解析>>

    科目：初中数学 来源：2017年安徽省中考数学三模试卷 题型：解答题

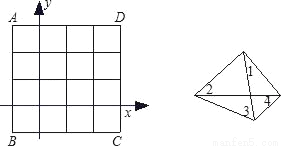
    如图，放在平面直角坐标系中的正方形ABCD的边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（如图，它有四个顶点，各顶点数分别是1、2、3、4），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的点数作为直角坐标系中点P的坐标（第一次的点数为横坐标，第二次的点数为纵坐标）．

    （1）求点P落在正方形面上（含边界，下同）的概率；

    （2）将正方形ABCD平移数个单位，是否存在一种平移，使点P落在正方形面上的概率为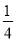？若存在，指出其中的一种平移方式；若不存在，说明理由．

    （1）；（2）． 【解析】【试题分析】 （1）列表格把每种情况都列举出来，看看满足条件的有几种，然后作比即可. （2）将正方形向左平移1个单位，向下平移1个单位就能够满足条件. 【试题解析】 （1）由图可知，点P落在正方形面上（含边界，下同）的情况是：（1，1），（2，1），（3，1），（1，2），（2，2），（3，2），（1，3），（2，3），（3，3）；概率是：9...

    查看答案和解析>>

    同步练习册答案