练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：(2m-3)(2m+5) -(4m-1).

    【解析】试题分析:先进行多项式乘法运算，然后再合并同类项即可. 试题解析：原式=.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省2017-2018学年度上期九年级数学第三次月考试卷 题型：填空题

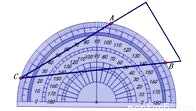
    将量角器按如图所示的方式放置在三角形纸板上，使顶点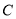在半圆上，点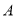、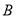的读数分别为100°、150°，则∠ACB的大小为______度．

    25 【解析】连接OA，OB，根据题意确定出∠AOB的度数，利用圆周角定理即可求出∠ACB的度数． 【解析】 连接OA，OB，由题意得：∠AOB=50°， ∵∠ACB与∠AOB都对， ∴∠ACB=∠AOB=25°， 故答案为：25 “点睛”此题考查了圆周角定理，熟练掌握圆周角定理是解本题的关键．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

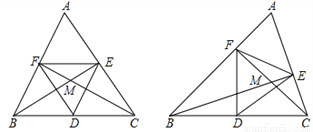
    如图，在△ABC中，∠A=60°，BE⊥AC，垂足为E，CF⊥AB，垂足为F，点D是BC的中点，BE，CF交于点M．

    （1）如果AB=AC，求证：△DEF是等边三角形；

    （2）如果AB≠AC，试猜想△DEF是不是等边三角形？如果△DEF是等边三角形，请加以证明；如果△DEF不是等边三角形，请说明理由.

    （1）证明见解析（2）△DEF是等边三角形． 【解析】试题分析：（1）先判定△ABC是等边三角形，再根据等腰三角形三线合一的性质可得EF=ED=DF，从而可得△DEF是等边三角形； （2）先根据直角三角形两锐角互余的性质求出∠ABE=∠ACF=30°，再根据三角形的内角和定理求出∠BCF+∠CBE=60°，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BDF+∠CDE=12...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型：单选题

    等腰三角形一腰上的高与另一腰的夹角为30o，则顶角的度数为（ ）

    A. 60o B. 120 o C. 60o或120o D. 60o或150o

    C 【解析】【解析】 如图（1），∵AB=AC，BD⊥AC，∴∠ADB=90°，∵∠ABD=30°，∴∠A=60°； 如图（2），∵AB=AC，BD⊥AC，∴∠BDC=90°，∵∠ABD=30°，∴∠BAD=60°，∴∠BAC=120°； 综上所述，它的顶角度数为：60°或120°．故选C．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年八年级上学期第二次统测数学试卷 题型：解答题

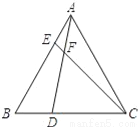
    如图，在等边△ABC中，点D、E分别在边BC、AB上，且BD=AE，AD与CE交于点F．

    （1）求证：AD=CE；

    （2）求∠DFC的度数．

    （1）证明见解析；（2）∠DFC=60°． 【解析】试题分析：（1）根据△ABC是等边三角形，得到∠BAC=∠B=60°，AB=AC，再根据AE=BD可以利用SAS证得△AEC≌△BDA，从而证得AD=CE． （2）根据△AEC≌△BDA得到∠ACE=∠BAD，然后求得∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°，从而求得其正弦值． 试题解析： 证明：（1）在...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年八年级上学期第二次统测数学试卷 题型：解答题

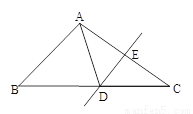
    如图，△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm．求△ABC的周长．

    见解析 【解析】试题分析：根据中垂线的性质得出AC=2AE=6，AD=CD，根据△ABD的周长求出AB+BC=13，然后计算出△ABC的周长. 试题解析：∵DE是AC的垂直平分线 ∴AD=CD AC=2AE=2×3=6 ∵△ABD的周长为13cm ∴AB+AD+BD=13 ∴AB+CD+BD=13 即AB+BC=13 ∴△ABC的周长=AB+BC+AC=13+6=19.

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年八年级上学期第二次统测数学试卷 题型：单选题

    下列各式中，计算正确的是（　　）

    A. （a﹣b）2=a2﹣b2 B. （2x﹣y）2=4x2﹣2xy+y2

    C. (a﹣3b）（a+3b）=a2﹣9b2 D. (15 x2 y-10x y2) ÷5xy=3x-2 y2

    C 【解析】A. （a﹣b）2=a2﹣ab+b2 ，故错误；B. （2x﹣y）2=4x2﹣4xy+y2，故错误；C. (a﹣3b）（a+3b）=a2﹣9b2，正确；D. (15 x2 y-10x y2) ÷5xy=3x-2 y，故错误， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测1 题型：填空题

    矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为　 　．

    3或6 【解析】试题分析： 由题意可知有两种情况，见图1与图2； 图1：当点F在对角线AC上时，∠EFC=90°， ∵∠AFE=∠B=90°，∠EFC=90°， ∴点A、F、C共线， ∵矩形ABCD的边AD=8， ∴BC=AD=8， 在Rt△ABC中，AC==10， 设BE=x，则CE=BC﹣BE=8﹣x， 由翻折的性质得，AF=AB=6...

    查看答案和解析>>

    科目：初中数学 来源：广东省2018届九年级上学期学业检测（二）数学试卷 题型：单选题

    下列图形中是中心对称图形的有(　　)个．

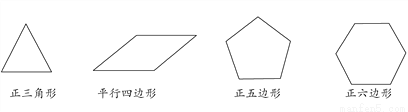
    A. 1 B. 2 C. 3 D. 4

    B 【解析】∵正三角形是轴对称能图形；平行四边形是中心对称图形；正五边形是轴对称图形；正六边形既是中心对称图形又是轴对称图形， ∴中心对称图形的有2个． 故选B.

    查看答案和解析>>

    同步练习册答案