
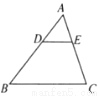
如图所示, 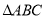 中,
中, 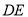 ∥
∥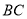 ,若
,若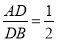 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 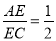 B.
B. 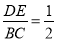 C.
C.  D.
D. 
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第2章 整式的加减 单元测试卷 题型:单选题
已知一个三角形的周长是3m-n,其中两边长的和为m+n-4,则这个三角形的第三边的长为( )
A. 2m-4 B. 2m-2n-4 C. 2m-2n+4 D. 4m-2n+4
C 【解析】由题意得 3m-n- (m+n-4) =2m-2n+4. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:单选题
下列命题中,真命题是( )
A. 对角线相等且互相垂直的四边形是菱形 B. 有一条对角线平分对角的四边形是菱形
C. 菱形是对角线互相垂直平分的四边形 D. 菱形的对角线相等
C 【解析】A、对角线相等且互相垂直的四边形不一定是菱形,故此选项错误; B、有一条对角线平分对角的四边形不一定是菱形,此选项错误; C、菱形是对角线是互相垂直平分的四边形,此选项正确; D、菱形的对角线不一定相等,此选项错误, 故选C.查看答案和解析>>
科目:初中数学 来源:福建省莆田市秀屿区2018届九年级上学期期末考试数学试卷 题型:解答题
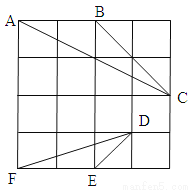
如图,在4×4的正方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC , BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:福建省莆田市秀屿区2018届九年级上学期期末考试数学试卷 题型:填空题
如果将抛物线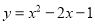 向上平移,使它经过点
向上平移,使它经过点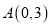 ,那么所得新抛物线的表达式是_______________.
,那么所得新抛物线的表达式是_______________.
查看答案和解析>>
科目:初中数学 来源:福建省莆田市秀屿区2018届九年级上学期期末考试数学试卷 题型:单选题
一元二次方程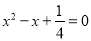 的根是( )
的根是( )
A. 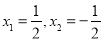 B.
B. 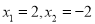
C. 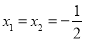 D.
D. 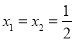
查看答案和解析>>
科目:初中数学 来源:人教版初中数学九年级上册第二十三章《图形的旋转》同步测试 题型:填空题
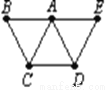
如图,△ABC、△ACD、△ADE 是三个全等的正三角形,那么△ABC 绕着顶点A沿逆时针方向至少旋转______度,才能与△ADE完全重合.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年河南省南阳市镇平县七年级(上)12月月考数学试 题型:解答题
计算:
(1)45﹣92+5﹣8;(2)( ﹣
﹣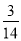 +
+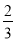 )×(﹣42);
)×(﹣42);
(3)2×(﹣5)+22﹣3÷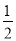 ;(4)﹣24+|6﹣10|﹣3×(﹣1)2014.
;(4)﹣24+|6﹣10|﹣3×(﹣1)2014.
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册 第十六章 《二次根式》复习测试 题型:解答题
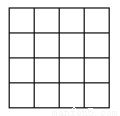
在如图的4×4的方格内画△ABC,使它的顶点都在格点上,三条边长分别为3, 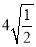 ,
, 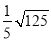 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com