练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

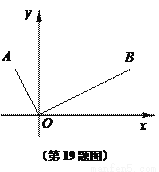
    如图在平面直角坐标系xOy中，O为坐标原点，点A的坐标为（－1，2），点B在第一象限，且OB⊥OA，OB=2OA，求经过A、B、O三点的二次函数解析式．

    【解析】试题分析：过点作轴于，过点作轴于，根据三角形相似求出点的坐标，再由待定系数法求出二次函数的解析式. 试题解析：过点作轴于，过点作轴于， 解得： 点的坐标为： 设二次函数的解析式为： 把点的坐标代入可得： 解得： 二次函数的解析式为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖北省孝感市八校联谊2017-2018学年八年级数学上册12月联考试卷 题型：解答题

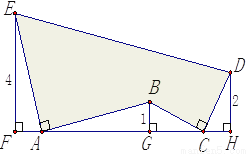
    如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中阴影部分的面积S是

    18 【解析】∵AE⊥AB且AE=AB，EF⊥FH，BG⊥FH， ∴∠EAB=∠EFA=∠BGA=90°，∠EAF+∠BAG=90°，∠ABG+∠BAG=90° ∴∠EAF=∠ABG， ∵AE=AB，∠EFA=∠AGB，∠EAF=∠ABG ∴△EFA≌△ABG ∴AF=BG，AG=EF． 同理证得△BGC≌△DHC得GC=DH，CH=BG． ∴FH=...

    查看答案和解析>>

    科目：初中数学 来源：2017年陕西省西安市中考数学模拟试卷 题型：解答题

    学校田径运动会快要举行了，小刚用自己积攒的零花钱买了一双运动鞋，顺便想研究一下鞋码与脚的大小之间的关系，于是，小刚回家量了一下妈妈36码的鞋子，内长是23cm；量了爸爸42码的鞋子，内长是26cm；又量了自己刚买的鞋子，内长是24.5cm；然后，又看了看自己所买的鞋的鞋码，可是怎么也搞不懂一双鞋子的鞋码与其内长到底是什么关系，带着这个问题小刚去问数学老师，数学老师说：设鞋内长是xcm，这鞋子的号码是y，那么y是x的一次函数，请你写出这个一次函数关系式，并算一算小刚买了鞋是多少码？

    y=2x﹣10，39码 【解析】试题分析：设y=kx+b（k≠0），然后把x=23时，y=36；x=26时，y=42代入得到关于k、b的方程组，解方程组得到k和b的值，确定一次函数关系式，然后令x=24.5，计算对应的y的值，就可得到刚买的鞋是多少码了． 试题解析：设y=kx+b（k≠0）， ∵当x=23时，y=36；当x=26时，y=42， ∴ ， 解得， ∴...

    查看答案和解析>>

    科目：初中数学 来源：2017年陕西省西安市中考数学模拟试卷 题型：单选题

    在下列几何体中，截面不是等腰梯形的是（　　）

    A. 圆台 B. 圆柱 C. 正方体 D. 三棱柱

    B 【解析】A、根据圆台的定义，即以直角梯形垂直于底边的腰所在直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫做圆台．那么它的截面一定是等腰梯形，故本选项不符合；B、根据圆柱的定义，即以矩形的一边所在的直线为旋转轴旋转而成，则它的截面一定是矩形，故本选项符合；C、正方体的截面可能是三角形、四边形、五边形、六边形，四边形中可能是等腰梯形，故本选项不符合；D、三棱柱的截面可能是等腰梯形，故...

    查看答案和解析>>

    科目：初中数学 来源：2017学年第一学期上海（闵行区）九年级数学质量调研试卷 题型：解答题

    抛物线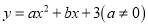经过点A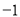（，0），B（，0），且与y轴相交于点C．

    （1）求这条抛物线的表达式；

    （2）求∠ACB的度数；

    （3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．

    （1）；（2）45°；（3）. 【解析】试题分析： 把点的坐标代入即可求得抛物线的解析式. 作BH⊥AC于点H，求出的长度，即可求出∠ACB的度数. 延长CD交x轴于点G，△DCE∽△AOC，只可能∠CAO=∠DCE.求出直线的方程，和抛物线的方程联立即可求得点的坐标. 试题解析：（1）由题意，得 解得． ∴这条抛物线的表达式为． （2）作BH⊥AC于点H...

    查看答案和解析>>

    科目：初中数学 来源：2017学年第一学期上海（闵行区）九年级数学质量调研试卷 题型：填空题

    已知在直角坐标平面内，以点P（1，2）为圆心，r为半径画圆，⊙P与坐标轴恰好有三个交点，那么r的取值是 ．

    2或 【解析】试题解析： ∵以点P(1,2)为圆心，r为半径画圆，与坐标轴恰好有三个交点， ∴⊙P与x轴相切(如图1)或⊙P过原点(如图2)， 当⊙P与x轴相切时，r=2； 当⊙P过原点时， ∴r=2或. 故答案为：2或.

    查看答案和解析>>

    科目：初中数学 来源：2017学年第一学期上海（闵行区）九年级数学质量调研试卷 题型：填空题

    如果，那么 ．

    【解析】试题解析： 设a=2t，b=3t， 故答案为:

    查看答案和解析>>

    科目：初中数学 来源：陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型：填空题

    已知点P（a，-3）在一次函数y=2x+9的图象上，则a=______．

    -6 【解析】∵点P（a，-3）在一次函数y=2x+9的图象上， ∴，解得： . 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：内蒙古赤峰市宁城县2018届九年级上学期期末数学试卷 题型：解答题

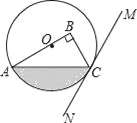
    如图，在Rt△ABC中，∠B=90°，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使∠BCM=2∠A．

    （1）判断直线MN与⊙O的位置关系，并说明理由；

    （2）若OA=4，∠BCM=60°，求图中阴影部分的面积．

    （1）相切；（2）． 【解析】试题分析：（1）MN是⊙O切线，只要证明∠OCM=90°即可．（2）求出∠AOC以及BC，根据S阴=S扇形OAC﹣S△OAC计算即可． 试题解析：（1）MN是⊙O切线． 理由：连接OC． ∵OA=OC， ∴∠OAC=∠OCA， ∵∠BOC=∠A+∠OCA=2∠A，∠BCM=2∠A， ∴∠BCM=∠BOC， ∵∠B=90°...

    查看答案和解析>>

    同步练习册答案