
已知方程3x2﹣19x+m=0的一个根是1,那么它的另一个根是 ,m= .
,16. 【解析】 试题分析:把方程的一个根代入方程,可以求出字母系数的值,然后根据根与系数的关系,由两根之和求出方程的另一个根. 【解析】 把1代入方程有: 3﹣19+m=0 ∴m=16. 设方程的另一个根是x,有两根之和有: x+1= ∴x=. 故答案分别是:,16.科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:填空题
在平面直角坐标系中,将抛物线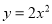 向上平移3个单位,得到的抛物线的函数表达式为 .
向上平移3个单位,得到的抛物线的函数表达式为 .
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
在△ABC中,AB=AC,点D为BC中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF
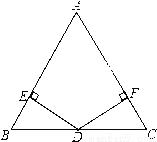
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列计算正确的是( )
A. 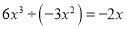 B.
B. 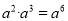 C.
C. 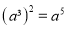 D.
D. 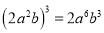
查看答案和解析>>
科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:解答题
⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=12cm,CD=16cm,求AB和CD之间的距离.
2cm或14cm 【解析】试题分析:分两种情况进行讨论:①弦和在圆心同侧;②弦和在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可. 试题解析:①当弦AB和CD在圆心同侧时,如图1所示, ∵AB=16cm,CD=12cm, ∴AE=8cm,CF=6cm, ∵OA=OC=10cm, ∴EO=6cm,OF=8cm, ∴EF=OF?OE=2cm; ...查看答案和解析>>
科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:单选题
如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58° , 则∠BCD度数为( )
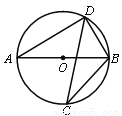
A.116° B.64° C.58° D.32°
D. 【解析】 试题解析:∵AB是⊙O的直径, ∴∠ADB=90°, ∵∠ABD=58°, ∴∠A=90°-∠ABD=32°, ∴∠BCD=∠A=32°. 故选D.查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
已知在平面直角坐标系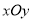 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点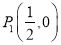 ,
,  ,
, 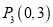 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与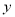 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标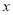 的取值范围.
的取值范围.
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径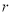 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:填空题
抛物线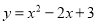 的对称轴方程是____________________.
的对称轴方程是____________________.
查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
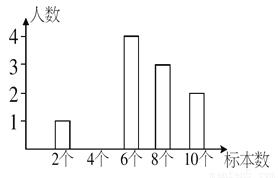
某生物课外活动小组的同学举行植物标本制作比赛,结果统计如下:

根据表中提供的信息,回答下列问题:
(1)该组共有学生多少人?
(2)每人制作标本数在6个及以上的人数在全组人数中所占比例?
(3)平均每人制作多少个标本?
(4)补全下图的条形统计图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com