
某校九年级举行毕业典礼,需要从九(1)班的2名男生1名女生、九(2)的1名男生1名女生共5人中选出2名主持人.
(1)用树形图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
【解析】 (1)画树状图得: 共有20种等可能的结果。 (2)∵2名主持人来自不同班级的情况有12种, ∴2名主持人来自不同班级的概率为: 。 (3)∵2名主持人恰好1男1女的情况有12种, ∴2名主持人恰好1男1女的概率为: 。 【解析】试题分析:(1)画出树状图或者列表可得所有可能情形共20种;(2)根据树状图可得:2名主持人来自不同班级的情况有12种,所...科目:初中数学 来源:北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型:单选题
若2x3-ax2-5x+5=(2x2+ax-1)(x-b)+3,其中a,b为整数,则a+b之值为何?( )
A. -4 B. -2 C. 0 D. 4
D 【解析】【解析】 ∵2x3-ax2-5x+5=(2x2+ax-1)(x-b)+3,∴2x3-ax2-5x+5=2x3+(a-2b)x2-(ab+1)x+b+3, ∴-a=a-2b,ab+1=5,b+3=5, 解得:b=2,a=2,∴a+b=2+2=4. 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型:单选题
下列运算中,正确的是( )
A. -2x(3x2y-2xy)=-6x3y-4x2y
B. 2xy2(-x2+2y2+1)=-4x3y4
C. (3ab2-2ab)·abc=3a2b3-2a2b2
D. (ab)2(2ab2-c)=2a3b4-a2b2c
D 【解析】解:A. -2x(3x2y-2xy)=-6x3y+4x2y,故A错误; B. 2xy2(-x2+2y2+1)= ,故B错误; C. (3ab2-2ab)·abc= ,故C错误; D. (ab)2(2ab2-c)=2a3b4-a2b2c,正确. 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 1.4 整式的乘法 多项式与多项式相乘 同步课时练习题 题型:填空题
在(ax+3y)与(x-y)的积中,不含xy项,则a必须为__.
3 【解析】【解析】 (ax+3y)(x-y)=ax2-axy+3xy-3y2=ax2+(-a+3)xy-3y2. ∵积中不含xy项,∴-a+3=0,解得a=3,∴常数a必须为3.故答案为:3.查看答案和解析>>
科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 1.4 整式的乘法 多项式与多项式相乘 同步课时练习题 题型:单选题
下列各式计算正确的是( )
A. (x+5)(x-5)=x2-10x+25 B. (2x+3)(x-3)=2x2-9
C. (3x+2)(3x-1)=9x2+3x-2 D. (x-1)(x+7)=x2-6x-7
C 【解析】试题解析:A、(x+5)(x-5)=x2-25,本选项错误; B、(2x+3)(x-3)=2x2-6x+3x-9=2x2-3x-9,本选项错误; C、(3x+2)(3x-1)=9x2-3x+6x-2=9x2+3x-2,本选项正确; D、(x-1)(x+7)=x2+7x-x-7=x2+6x-7,本选项错误. 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版九年级上册数学全册综合测试卷一 题型:填空题
方程x2﹣4=0的解是___________.
x=2或-2 【解析】x2﹣4=0, (x-2)(x+2)=0, 所以x1=2,x2=-2.查看答案和解析>>
科目:初中数学 来源:北师大版九年级上册数学全册综合测试卷一 题型:单选题
如图,在△ABC中,若DE∥BC,AD∶BD=1∶2,若△ADE的面积等于2,则△ABC的面积等于

A.6 B.8 C.12 D.18
D 【解析】 试题分析:由DE∥BC可得△ADE∽△ABC,再根据相似三角形的性质即可求得结果. ∵DE∥BC ∴△ADE∽△ABC ∵AD∶BD=1∶2 ∴AD∶AB=1∶3 ∴∶∶9 ∵ ∴ 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册 同步测试 1.3 同底数幂的除法 题型:单选题
下列运算结果正确的是( )
A. x6÷x2=x3 B. (﹣x)﹣1=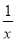 C. (2x3)2=4x6 D. ﹣2a2•a3=﹣2a6
C. (2x3)2=4x6 D. ﹣2a2•a3=﹣2a6
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第21章 一元二次方程 单元测试卷 题型:单选题
若关于x的方程(a+1)x2+2x-1=0是一元二次方程,则a的取值范围是( )
A. a≠-1 B. a>-1 C. a<-1 D. a≠0
A 【解析】根据一元二次方程的定义可得a+1≠0,即a≠-1,故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com