练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

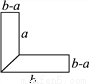
    小红家有一块L型的菜地，如图所示，要把L型的菜地按图那样分成面积相等的梯形种上不同的蔬菜，这两个梯形的上底都是am，下底都是bm，高都是(b－a)m，请你帮小红家算一算这块菜地的面积共有多少？并求出当a＝10m，b＝30m时，L型菜地的总面积．

    b2－a2，800 m2 【解析】试题分析：（1）根据梯形的面积公式列出代数式，然后根据整式的乘法公式进行计算； （2）只需把字母的值代入（1），计算即可． 试题解析：【解析】 （1）小红家的菜地面积共有： ； （2）当a=10米，b=30米时，原式=302-102=900-100=800（平方米）．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：单选题

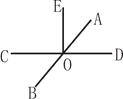
    如图，直线EO⊥CD，垂足为点O，AB平分∠EOD，则∠BOD的度数为（ ）

    A. 120° B. 130°

    C. 135° D. 140°

    C 【解析】试题分析：根据直线EO⊥CD，可知∠EOD=90°，根据AB平分∠EOD，可知∠AOD=45°，再根据邻补角的定义即可求出∴∠BOD=180°-45°=135°

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.2幂的乘方与积的乘方 第1课时 幂的乘方 同步练习 题型：单选题

    若5x=125y,3y=9z,则x∶y∶z等于(　　)

    A. 1∶2∶3 B. 3∶2∶1 C. 1∶3∶6 D. 6∶2∶1

    D 【解析】∵， ， ∴x=3y，y=2z，即x=3y=6z； 设z=k，则y=2k，x=6k；（k≠0） ∴x：y：z=6k：2k：k=6：2：1． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：解答题

    解方程:2x(x-1)=12+x(2x-5).

    x=4 【解析】试题分析：先用单项式乘多项式法则计算，然后移项，合并同类项，化系数为1即可． 试题解析：【解析】 去括号得：2x2-2x=12+2x2-5x， 移项、合并同类项得：3x=12， 系数化为1得：x=4．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：单选题

    下列计算错误的是(　　)

    A. -3x(2-x)=-6x+3x2

    B. (2m2n-3mn2)(-mn)=-2m3n2+3m2n3

    C. xy(x2y-xy2-1)=x3y2-x2y3

    D. 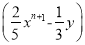xy=xn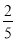+2y-xy2

    C 【解析】解：A． -3x(2-x)=-6x+3x2，正确； B． (2m2n-3mn2)(-mn)=-2m3n2+3m2n3，正确； C． xy(x2y-xy2-1)=x3y2-x2y3-xy，故C错误； D． xy=xn+2y-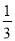xy2，正确． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 1.4 整式的乘法 多项式与多项式相乘 同步课时练习题 题型：填空题

    计算：(1)(2x＋3)(x－2)＝__________；(2)(3a－2)(2a＋5)＝________________.

    2x2－x－6 6a2＋11a－10 【解析】【解析】 （1）原式=2x2-x-6； （2）原式=6a2+11a-10． 故答案为：(1) 2x2－x－6； (2) 6a2＋11a－10．

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 1.4 整式的乘法 多项式与多项式相乘 同步课时练习题 题型：单选题

    计算(2x2－4)(2x－1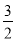－x)的结果，与下列哪一个式子相同？( )

    A. －x2＋2 B. x3＋4

    C. x3－4x＋4 D. x3－2x2－2x＋4

    D 【解析】【解析】 原式=．故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上册数学全册综合测试卷一 题型：单选题

    函数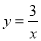是（　　）

    A. 一次函数 B. 二次函数 C. 反比例函数 D. 正比例函数

    C 【解析】函数是反比例函数. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第21章 一元二次方程 单元测试卷 题型：解答题

    关于x的一元二次方程x2＋(2k＋1)x＋k2＋1＝0有两个不等实根x1，x2.

    (1)求实数k的取值范围；

    (2)若方程两实根x1，x2满足|x1|＋|x2|＝x1·x2，求k的值．

    (1) k＞；(2)k=2 【解析】试题分析：（1）根据根与系数的关系得出△＞0，代入求出即可； （2）根据根与系数的关系得出x1+x2=﹣（2k+1），x1•x2=k2+1，根据x1+x2=﹣x1•x2得出﹣（2k+1）=﹣（k2+1），求出方程的解，再根据（1）的范围确定即可． 试题解析：（1）∵原方程有两个不相等的实数根， ∴△=（2k+1）2﹣4（k2+1）＞0， ...

    查看答案和解析>>

    同步练习册答案