练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知△ABC的三条边长分别为3，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（　　）

    A. 6条 B. 7条 C. 8条 D. 9条

    B 【解析】试题分析：利用等腰三角形的性质分别利用AB，AC为底以及为腰得出符合题意的图形即可． 【解析】 如图所示：当BC1=AC1，AC=CC2，AB=BC3，AC4=CC4，AB=AC5，AB=AC6，BC7=CC7时，都能得到符合题意的等腰三角形． 故选：B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册4.3.2探索三角形全等的条件练习 题型：解答题

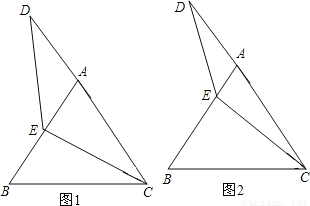
    等边△ABC中，点E在AB上，点D在CA的延长线上，且ED=EC．试探索以下问题：

    （1）如图1，当E为AB中点时，试确定线段AD与BE的大小关系，请你直接写出结论：AD BE；

    （2）如图2，若点E为线段AB上任意一点，（1）中结论是否成立，若成立，请证明结论，若不成立，请说明理由。

    （1）AD=BE；（2）证明见解析 【解析】分析：(1)根据题意易得∠D=∠AED=30°,即可得AD=AE,再根据AE=BE,即可解题; (2)通过作EF∥AC构造等边三角形把BE转化为EF,再利用“角角边”易证△AED≌△FCE,可得AD=FE,即可解题. 本题解析： （1）AD=BE； （2）过点E作EF∥AC交BC于点F， ∴∠EFB=∠ACB，∠BEF...

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如图:

    (1)求所捂的二次三项式;

    (2)若x=1,求所捂二次三项式的值.

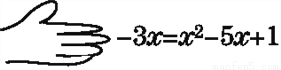
    （1）x2-2x+1.（2）0. 【解析】试题分析：（1）本题考查了整式的加减，根据被减数=差+减数列式计算即可；（2）把x=1代入（1）中所求出的式子计算求值. 解:(1)设所捂的二次三项式为A, 根据题意得A=x2-5x+1+3x=x2-2x+1. (2)当x=1时,原式=(x-1)2=(1-1)2=0.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：解答题

    已知△ABC的两边长分别为3和7,第三边的长是关于x的方程=x+1的解,求a的取值范围.

    6

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    下列长度的三根小木棒能构成三角形的是( )

    A. 2 cm，3 cm，5 cm B. 7cm，4 cm，2 cm

    C. 3 cm，4 cm，8 cm D. 3 cm，3 cm，4 cm

    D 【解析】A选项：2+3＝5，故不能构成三角形； B选项：4+2<7，故不能构成三角形； C选项：3+4<8,故不能构成三角形； D选项：3+3〉4，故能构成三角形. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：解答题

    已知AD是△ABC的高,∠BAD=72°,∠CAD=21°,求∠BAC的度数.

    93°; 51° 【解析】试题分析：分高AD在△ABC内部和外部两种情况讨论求解即可． 试题解析：【解析】 ①如图1，当高AD在△ABC的内部时，∠BAC=∠BAD+∠CAD=72°+21°=93°； ②如图2，当高AD在△ABC的外部时，∠BAC=∠BAD﹣∠CAD=72°﹣21°=51°． 综上所述：∠BAC的度数为93°或51°．故答案为：93°或51°．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：单选题

    过△ABC的顶点A,作BC边上的高,以下作法正确的是(　　)

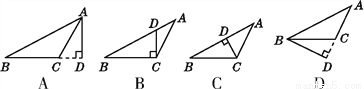
    A. A B. B C. C D. D

    A 【解析】【解析】 △ABC中BC边上的高正确的是A选项．故选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：单选题

    把等腰直角三角形的三角板按如图所示的方式立在桌面上，顶点A顶着桌面，若另两个顶点分别距离桌面5cm和3cm，则过另外两个顶点向桌面作垂线，则垂足之间的距离即DE的长为( )

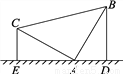
    A. 4cm B. 6cm C. 8cm D. 求不出来

    C 【解析】∵ ∠BAC=90° ∠AEC=90° ∴ ∠BAC=∠AEC ∵ ∠DAB+∠BAC=∠DAC ∠ECA+∠AEC=∠DAC ∠BAC=∠DEC ∴ ∠ECA=∠DAB ∵ △ABD是直角三角形 △CAE是直角三角形 AB=AC ∠ECA=∠DAB ∴ △ABD≌△CAE (一边一锐角对应相等的两个直角三角形全等) ∴ AE=BD AD=CE...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    在一条笔直的高速公路上依次有3个标志点A、B、C，甲、乙两车分别从A、C两点同时出发，匀速行驶，甲车从A→B→C，乙车从C→B→A，甲、乙两车离B的距离y1、y2（千米）与行驶时间x（小时）之间的函数关系图象如图所示．观察图象，给出下列结论：①A、C之间的路程为690千米；②乙车比甲车每小时快30千米；③4.5小时两车相遇；④点E的横坐标表示两车第二次相遇的时间；⑤点E的坐标为（7，180）其中正确的有________（把所有正确结论的序号都填在横线上）．

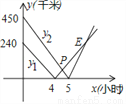
    ①②⑤ 【解析】试题解析：①450+240=690（千米）． 故A、C之间的路程为690千米是正确的； ②450÷5-240÷4 =90-60 =30（千米/小时）． 故乙车比甲车每小时快30千米是正确的； ③690÷（450÷5+240÷4） =690÷（90+60） =690÷150 =4.6（小时）． 故4.6小时两车相遇，原...

    查看答案和解析>>

    同步练习册答案