练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

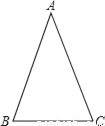
    写出下列命题的已知、求证，并完成证明过程．

    命题：如果一个三角形的两条边相等，那么两条边所对的角也相等（简称：“等边对等角”．）

    已知：　 　．

    求证：　 　．

    证明：

    答案见解析. 【解析】试题分析：根据图示，分析原命题，找出其条件与结论，然后根据AB=AC，结合全等三角形的性质，从而得出结论． 试题解析：【解析】 已知：在△ABC中，AB=AC，求证：∠B=∠C． 证明：过点A作AD⊥BC于D，∴∠ADB=∠ADC=90°．在Rt△ABD和Rt△ACD中，∵AB=AC，AD=AD，∴Rt△ABD≌Rt△ACD（HL），∴∠B=∠C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

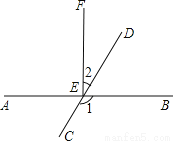
    科目：初中数学 来源：江苏省2016-2017学年七年级上学期期末考试数学试卷 题型：填空题

    如图，直线AB与CD相交于E点，EF⊥AB，垂足为E，∠1=125°，则∠2的度数是__________．

    35° 【解析】∵直线AB与CD相交于E，∠1=125°， ∴∠AED=∠1=125°， ∵EF⊥AB， ∴∠AEF=90°， ∴∠2=∠AED-∠AEF=125°-90°=35°.

    查看答案和解析>>

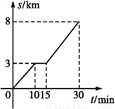
    科目：初中数学 来源：2017-2018学年北师大版七年级数学下册 期中测评 题型：解答题

    小明家距离学校8 km,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.

    请根据图象,解答下列问题:

    (1)小明行了多少千米时,自行车出现故障?修车用了几分钟?

    (2)小明共用了多少时间到学校的?

    (3)小明修车前、后的行驶速度各是多少?

    (4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?

    (1) 5(min)；(2)小明共用了30 min到学校；(3) (km/min)；(4) 3.3(min)． 【解析】试题分析：（1）（2）（3）（4）先观察横坐标表示的意义，求速度利用v=,可得. 试题解析： (1)由题图可知,小明行了3 km时,自行车出现故障,修车用了15-10=5(min). (2)小明共用了30 min到学校. (3)修车前速度:3÷10=...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学下册 期中测评 题型：单选题

    在一个数值转换机中（如图），当输入x=-5时，输出的y值是

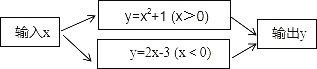
    A．26 B．-13 C．-24 D．7

    B． 【解析】 试题解析：将x=-5代入y=2x-3，得 y=2×（-5）-3=-10-3=-13， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省泰州市中考数学三模试卷 题型：解答题

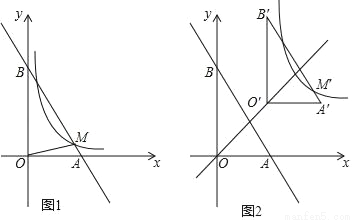
    如图1，已知一次函数y=ax+2与x轴、y轴分别交于点A、B，反比例函数y=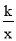经过点M．

    （1）若M是线段AB上的一个动点（不与点A、B重合）．当a=﹣3时，设点M的横坐标为m，求k与m之间的函数关系式．

    （2）当一次函数y=ax+2的图象与反比例函数y=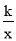的图象有唯一公共点M，且OM=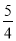，求a的值．

    （3）当a=﹣2时，将Rt△AOB在第一象限内沿直线y=x平移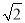个单位长度得到Rt△A′O′B′，如图2，M是Rt△A′O′B′斜边上的一个动点，求k的取值范围．

    （1）k=﹣3m2+2m（0＜m＜）；（2）a=±；（3）k的取值范围是2≤k≤3． 【解析】试题分析：（1）把a=﹣3代入一次函数y=ax+2，与反比例函数组成方程组，用m表示k即可； （2）根据△=0，得k=﹣，利用勾股定理解得a的值； （3）当a=﹣2时，y=﹣2x+2，得点A的坐标为（1，0），点B的坐标为（0，2），由OO'为沿直线y=x平移，可知：O向上平移一个单位，...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省泰州市中考数学三模试卷 题型：填空题

    抛物线y=mx2﹣2mx+m﹣3（m＞0）在﹣1＜x＜0位于x轴下方，在3＜x＜4位于x轴上方，则m的值为_____．

    【解析】【解析】 ∵抛物线y=mx2﹣2mx+m﹣3（m＞0）的对称轴为直线x=1，而在3＜x＜4位于x轴上方，∴抛物线在﹣2＜x＜﹣1这一段位于x轴的上方，∵在﹣1＜x＜0位于x轴下方，∴抛物线过点（﹣1，0），把（﹣1，0）代入y=mx2﹣2mx+m﹣3得m+2m+m﹣3=0，解得m=，故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省泰州市中考数学三模试卷 题型：填空题

    化简： ﹣3的结果是_____．

    【解析】【解析】 原式==．故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型：填空题

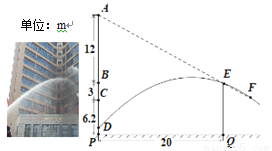
    两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F处出现火灾，此时A,E,F在同一直线上.跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同，现消防员将水流抛物线向上平移0.4m，再向左后退了____m，恰好把水喷到F处进行灭火．

    【解析】设直线AE的解析式为:y=kx+21.2. 把E（20,9.2）代入得， 20k+21.2=9.2, ∴k=-0.6, ∴y=-0.6x+21.2. 把y=6.2代入得， -0.6x+21.2=6.2， ∴x=25, ∴F(25,6.2). 设抛物线解析式为：y=ax2+bx+1.2, 把E（20,9.2）, F(25,6.2)代...

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古通辽市八年级（下）期末数学试卷 题型：解答题

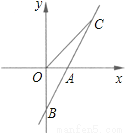
    如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．

    （1）求直线AB的解析式；

    （2）若直线AB上的点C在第一象限，且S△BOC=2，求点C的坐标．

    （1）直线AB的解析式为y=2x﹣2；（2）点C的坐标是（2，2）. 【解析】试题分析：（1）设直线的解析式为 将点点分别代入解析式即可组成方程组，从而得到的解析式； （2）设点的坐标为 根据三角形面积公式以及求出的横坐标，再代入直线即可求出的值，从而得到其坐标． 试题解析：(1)设直线AB的解析式为y=kx+b(k≠0). ∵直线AB过点A(1,0)、点B(0,?2)， ...

    查看答案和解析>>

    同步练习册答案