
不等式1﹣3(x﹣1)<8﹣x的负整数解是_____.
-1 【解析】试题解析:1?3(x?1)<8?x, 去括号得:1?3x+3<8?x, 移项得:?3x+x<8?1?3, 合并同类项得:?2x<4, 把x的系数化为1得:x>?2, 故负整数解为:?1. 故答案为:?1.科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
下图是一个六角棱栓,它的主视图和俯视图都正确的是( )

A. 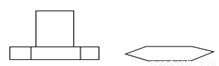 B.
B. 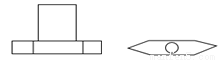
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:填空题
如图,小量角器的零度线在大量角器的零度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在小量角器上对应的度数为65°,那么在大量角器上对应的度数为_____度(只需写出0°~90°的角度).
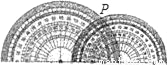
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
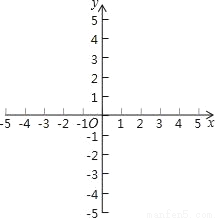
已知抛物线y=ax2+bx+c(a≠0)与x轴交于不同的两个点A(x1,0)和点B(x2,0)与y轴的正半轴交于点C,如果x1,x2是方程x2﹣2x﹣3=0的两个根(x1<x2),且图象经过点(2,3)
(1)求抛物线的解析式并画出图象
(2)x在什么范围内函数值y大于3且随x的增大而增大.
(3)设(1)中的抛物线顶点为D,在y轴上是否存在点P,使得DP+BP的和最小?若存在,求出这个最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
化简: 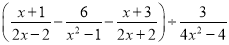 .
.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:单选题
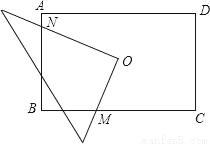
如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N.如果AB=4,AD=6,OM=x,ON=y.则y与x的关系是( )
A. 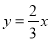 B.
B. 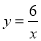 C. y=x D.
C. y=x D. 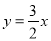
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:单选题
下列各组图形,可以经过平移变换由一个图形得到另一个图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:填空题
二次函数y=x2﹣2x+6的最小值是____.
5 【解析】试题分析:y=x2﹣2x+6=x2﹣2x+1+5 =(x﹣1)2+5, 可见,二次函数的最小值为5.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:填空题
按图9的方式摆放餐桌和椅子(每个小半圆代表1把椅子),n张餐桌子按上述方式拼在一起可摆放_____________把椅子(用含n的代数式表示).
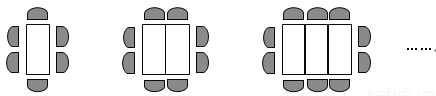
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com