
有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?
(1);(2)不公平,理由见解析. 【解析】试题分析:(1)列表列出所有等可能结果,根据概率公式解答即可; (2)由积为偶数的有8种情况,而积为奇数的有4种情况,即可判断. 试题解析:【解析】 (1)列表如下: ∵总结果有12种,其中积为6的有2种,∴P(积为6)=. (2)游戏不公平,因为积为偶数的有8种情况,所以概率是,而积为奇数的有4种情况,概率是,获胜的概率... 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:填空题
当x=_____时,式子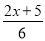 与
与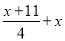 的值互为相反数.
的值互为相反数.
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:解答题
如图,已知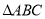 中,
中, 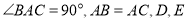 是
是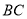 边上的点,将
边上的点,将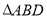 绕点
绕点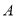 旋转,得到
旋转,得到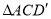 .
.
(1)当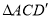 时,求证:
时,求证: 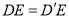 .
.
(2)在(1)的条件下,猜想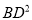 ,
, 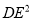 ,
, 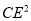 有怎样的数量关系,并说明理由.
有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
下列说法中正确的是( )
A. 两个直角三角形全等 B. 两个等腰三角形全等
C. 两个等边三角形全等 D. 两条直角边对应相等的直角三角形全等
D 【解析】试题解析:A、两个直角三角形只能说明有一个直角相等,其他条件不明确,所以不一定全等,故本选项错误; B、两个等腰三角形,腰不一定相等,夹角也不一定相等,所以不一定全等,故本选项错误; C、两个等边三角形,边长不一定相等,所以不一定全等,故本选项错误; D、它们的夹角是直角相等,可以根据边角边定理判定全等,正确. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:解答题
如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=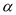 ,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用
,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用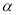 表示出直线BE、DF形成的锐角
表示出直线BE、DF形成的锐角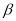 .
.
查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:填空题
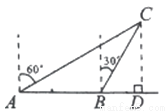
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_______海里.
查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
在平面直角坐标系中,将抛物线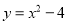 先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )
先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )
A. 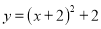 B.
B. 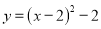 C.
C. 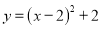 D.
D. 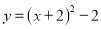
查看答案和解析>>
科目:初中数学 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
用适当的方法解下列方程:
(1)x2-7x+6=0; (2)(5x-1)2=3(5x-1);
(3)2x2-2x+3=0.
(1)x1=6,x2=1;(2)x1=,x2=;(3)方程无解. 【解析】试题分析:(1)利用十字相乘法将左边分解因式,然后利用因式分解法解方程; (2)把方程右边移至左边,提出公因式(5x-1),利用因式分解法解方程; (3)利用公式法求解,先计算根的判别式可得△<0,可得方程无解. 【解析】 (1)(x-6)(x-1)=0, x-6=0或x-1=0, x1...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期第二次月考数学试卷 题型:填空题
国家体育场“鸟巢”的建筑面积达258000m2,它用科学记数法表示应为 m2.
【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数。所以258000=2.58×105.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com