
关于x的方程2x2-ax+1=0一个根是1,则a的值是________;
3 【解析】把x=1代入方程2x2-ax+1=0得:2-a+1=0,解得:a=3, 故答案为:3.科目:初中数学 来源:江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在平面直角坐标系内它的大致图象是( )
A. 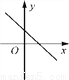 B.
B. 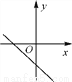 C.
C. 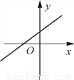 D.
D. 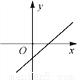
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:填空题
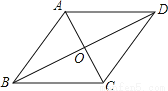
如图,菱形ABCD的周长为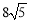 ,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO= ,菱形ABCD的面积S= .
,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO= ,菱形ABCD的面积S= .
查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:解答题
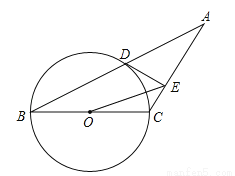
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:解答题
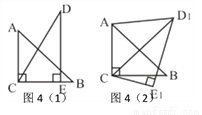
如图4(1),把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5。把三角板DCE绕着点C 顺时针旋转15°得到△D1CE1(如图(2)),此时 AB与CD1交于点O,则线段AD1的长度为______。
查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:单选题
用配方法解方程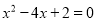 ,下列配方正确的是( )
,下列配方正确的是( )
A. 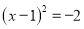 B. (x-2)2=2 C. (x+2)2=2 D. (x-2)2=6
B. (x-2)2=2 C. (x+2)2=2 D. (x-2)2=6
查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:解答题
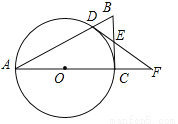
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
在平面直角坐标系中,点A的坐标为(-1, 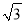 ),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
A. (0,-2) B. (1,- 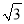 ) C. (2,0) D. (
) C. (2,0) D. (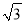 ,-1)
,-1)
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
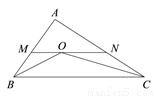
如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com