
��֪�����κ���y=ax2+bx+c��x��Ľ���Ϊ��x1��0������x2��0������x1��x2��������ax2+bx+c��a=0������Ϊm��n��m��n����������˵����ȷ���ǣ�������
A. x1+x2��m+n B. m��n��x1��x2 C. x1��m��n��x2 D. m��x1��x2��n
D ���������������� ����������� �ٵ�a��0ʱ�������߿������ϣ���ͼ1�� �߷���ax2+bx+c��a=0������Ϊm��n��m��n���� ax2+bx+c=a�� ����y=aʱ����ֱ���������ߵĽ���ĺ�����ֱ�Ϊm��n�� ��ͼ�εã�m��x1��x2��n�� �ڵ�a��0�������߿������£���ͼ2�� ��ͼ�εã�m��x1��x2��n�� ����������m��x1��x2��... ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�����ɹų����������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
������2.30��ʾ��ȷ��a�ķ�Χ��(�� )
A. 2.295��a��2.305 B. 2.25��a��2.35 C. 2.295��a��2.305 D. 2.25��a��2.35
A �����������������������2.30����ʾ��ȷ��a�ķ�ΧΪ2.295��a��2.305�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩģ����ѧ�Ծ� ���ͣ������
���ʵ��ķ��������з��̡�
(1)3x(x+3)=2(x+3)
(2)2x2?4x?3=0.
(1)x1=?3,x2= (2) �������������������С������ʽ�ֽⷨ����С���ù�ʽ��. �������������1��3x(x��3)-2(x��3)=0�� (x��3)(3x-2)=0�� �� ��2�� �� ��x1��1����x2��1��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶���ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ������
��������ͨ�¹ʷ�����������������ͨ�����Ϊ�ش��������⣬۶��������ѧ��ȤС��Ϊ����������ٶ����������ʵ�飺��ͼ���ڹ�·MN�����ƿ���ֱ�ߣ���ѡȡһ��C�����C����·�ľ���Ϊ30�ף�����MN��ѡȡA��B���㣬��á�CAN=30�㣬��CBN=60�㣮
��1����AB�ij�������ȷ��0.1�ף��ο�����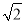 =1.41��
=1.41�� 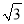 =1.73��
=1.73��
��2������·���������ٶ�Ϊ40ǧ��/Сʱ��ij����A��B��ʱ3�룬�ó��Ƿ��٣�
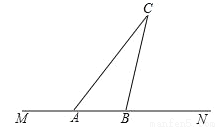
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶���ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ������
�������ֱ��Ϊ1��Բ����ˮ�ܵ���ˮ���Ϊ0.8�ף�����ˮ�ܵ��������ˮ��Ϊ______��
0.2��0.8�ף� ����������Ϊ��������� ����ͼ1��ʾ������OA����O��OC��AB�ڵ�D�� ��OC��AB��AB=0.8�ף� ��AD=AB=��0.8=0.4�ף� ��Բ����ˮ�ܵ���ֱ��Ϊ1�ף� ��OA=OC=0.5�ף� ��Rt��OAD�У�OD==0.3���ף��� ��CD=OC��OD=0.5��0.3=0.2���ף��� ����ͼ2��ʾ��CD=0.5+0....�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶���ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ���ѡ��
������ͼ���У������ĶԳ�ͼ�ζ�������Գ�ͼ�ε��ǣ�������
A. Բ B. �ȱ������� C. ���� D. ƽ���ı���
D ���������������� ѡ��A�������ĶԳ�ͼ�Σ�Ҳ����Գ�ͼ�Σ��ʴ�ѡ����� ѡ��B���������ĶԳ�ͼ�Σ�����Գ�ͼ�Σ��ʴ�ѡ����� ѡ��C���������ĶԳ�ͼ�Σ�����Գ�ͼ�Σ��ʴ�ѡ����� ѡ��D�������ĶԳ�ͼ�Σ�������Գ�ͼ�Σ��ʴ�ѡ����ȷ�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶����ѧ�ڶ��¡�һԪ���η��̡���Ԫ���� ���ͣ������
�ⷽ�̣�
(1)(x��8)2��36�� (2)x(5x��4)��(4��5x)��0��
(3)x2��3��3(x��1)�� (4)2x2��x��1��0.
(1)x1=-2, x2=-14; (2) X1=1, ��(3) x1=3�� x2=0 �� (4) . �������������������1������ֱ�ӿ�ƽ����.(2)������ʽ�ֽⷨ.(3) ������ʽ�ֽⷨ.(4)����ʮ����˷�. ��������� �ⷽ�̣�(1)(x��8)2��36�� x��8��6, . (2)x(5x��4)��(4��5x)��0�� (4��5x)(x-1)=0, ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩����ĩ����� ���ͣ������
��ͼ���ڡ�ABC�У���ACB��90�㣬CD��AB��D��AEƽ�֡�BAC���ֱ���BC��CD����E��F��EH��AB��H������FH.��֤���ı���CFHE�����Σ�
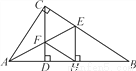
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������Դ��2016-2017ѧ����꼶����ĩ������ѧ�Ծ����� ���ͣ���ѡ��
��ͼ����֪AB�ǡ�O��ֱ����AD�С�O�ڵ�A����C�ǻ�EB���е㣬�����н��ۣ�
��OC��AE����EC��BC���ۡ�DAE����ABE����AC��OE��������ȷ���У�������
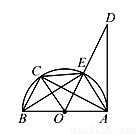
A. 1�� B. 2�� C. 3�� D. 4��
C �������������������CΪ���е㣬���ô����������涨���ó�OC��BE����ABΪԲ��ֱ��������ֱ�����Ե�Բ�ܽ�Ϊֱ�ǵõ�AE��BE������ȷ����OC��AE����A��ȷ�� ��CΪ���е㣬�������õȻ��Ե��ң��õ�BC=EC����B��ȷ�� ��ADΪԲ�����ߣ��õ�AD��OA������ȷ����һ�Խǻ��࣬����ֱ��������ABE������ǻ��࣬����ͬ�ǵ������ȣ��õ���DAE=��ABE����C��ȷ�� A...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com