练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1 ______ y2．（填“＞”“＜”或“=”）

    ＜ 【解析】试题解析：∵一次函数y=2x+1中k=2＞0， ∴y随x的增大而增大， ∵x1＜x2， ∴y1＜y2．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年陕西师大附中中考数学二模试卷 题型：填空题

    请从以下两个小题中任选一题作答，若多选，则按所选的第一题计分．

    A．正五边形的一个外角的度数是_____．

    B．比较大小：2tan71°_____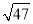（填“＞”、“=”或“＜”）

    72° ＜ 【解析】试题解析：A．360°÷5=72°． 答：正五边形的一个外角的度数是72°． B．∵2tan71°≈5.808， ≈6.856， ∴2tan71°＜． 故答案为：72°；＜．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷 题型：解答题

    如图，AB=DC，AC=DB，求证：AB∥CD．

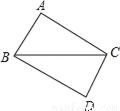
    详见解析. 【解析】本题考查的是全等三角形的判定与性质、平行线的判定， 先根据“SSS”证得△ABC≌△DCB，即可得到∠ABC=∠DCB，从而得到AB∥CD． ∵ 在△ABC和△DCB中， ， ∴ △ABC≌△DCB（SSS）． ∴ ∠ABC=∠DCB． ∴ AB∥CD．

    查看答案和解析>>

    科目：初中数学 来源：2017年浙江省台州市中考数学二模试卷 题型：解答题

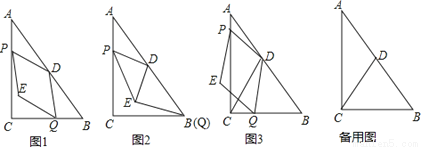
    如图1，Rt△ABC中，∠ACB=Rt∠，AC=8，BC=6，点D为AB的中点，动点P从点A出发，沿AC方向以每秒1个单位的速度向终点C运动，同时动点Q从点C出发，以每秒2个单位的速度先沿CB方向运动到点B，再沿BA方向向终点A运动，以DP，DQ为邻边构造?PEQD，设点P运动的时间为t秒．

    （1）当t=2时，求PD的长；

    （2）如图2，当点Q运动至点B时，连结DE，求证：DE∥AP.

    （3）如图3，连结CD．

    ①当点E恰好落在△ACD的边上时，求所有满足要求的t值；

    ②记运动过程中?PEQD的面积为S，?PEQD与△ACD的重叠部分面积为S1，当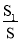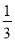＜时，请直接写出t的取值范围是 ______ ．

    （1）（2）证明见解析（3）①分三种情况讨论：满足要求的t的值为或或．②当＜时， t的取值范围是＜t＜． 【解析】（1）如图1中，作DF⊥CA于F， 当t=2时，AP=2，DF=AD•sinA=5×=3， ∵AF=AD•cosA=5×=4， ∴PF=4-2=2， ∴PD===． （2）如图2中， 在平行四边形PEQD中， ∵PE∥DQ， ∴PE...

    查看答案和解析>>

    科目：初中数学 来源：2017年浙江省台州市中考数学二模试卷 题型：解答题

    计算： ．

    【解析】试题分析：将特殊角的三角函数值代入求解． 试题解析： 原式= ＝ ＝

    查看答案和解析>>

    科目：初中数学 来源：2017年浙江省台州市中考数学二模试卷 题型：单选题

    如图，CD是⊙O的弦，O是圆心，把⊙O的劣弧沿着CD对折，A是对折后劣弧上的一点，∠CAD=100°，则∠B的度数是（　　）

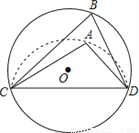
    A. 100° B. 80° C. 60° D. 50°

    B 【解析】试题分析：如图，翻折△ACD，点A落在A′处，可知∠A=∠A′=100°，然后由圆内接四边形可知∠A′+∠B=180°，解得∠B=80°. 故选：B

    查看答案和解析>>

    科目：初中数学 来源：四川省西昌市航天学校2017-2018学年七年级上册数学期中测试卷（含答案） 题型：解答题

    将1，2，…，2014这2014个正整数任意分成1007组，每组两个数，分别记作．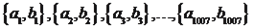

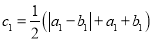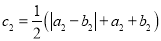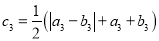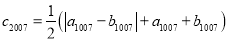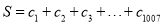    若， ， …， ．设，求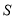的最大值和最小值，并给出相应的分组方案．

    ， ，分组见解析. 【解析】试题分析:先讨论a,b的关系,分别得出代数式的值,进而得出规律,然后可以以此规律可得出符合题意的组合,求解即可. 试题解析: , 此时的分组为, , 此时的分组为.

    查看答案和解析>>

    科目：初中数学 来源：四川省西昌市航天学校2017-2018学年七年级上册数学期中测试卷（含答案） 题型：填空题

    圆周率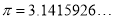，取近似值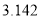，是精确到____位．

    0.001（或千分位） 【解析】因为的小数单位是0.001(或千分位),所以近似值,是精确到0.001(或千分位),故答案为: 0.001(或千分位).

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017年中考数学二模试卷 题型：填空题

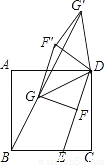
    如图，正方形ABCD中，E为BC上一点，BE=2CE，连接DE，F为DE中点，以DF为直角边作等腰Rt△DFG，连接BG，将△DFG绕点D顺时针旋转得△DF′G′，G′恰好落在BG的延长线上，连接F′G，若BG=2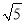，则S△GF′G′=________．

    【解析】【解析】 如图，作GM⊥BC于M，MG的延长线交AD于N，作DK⊥BG′于K，作KQ⊥DG′于Q，作F′H′BG′于H，BG′交AD于P． ∵BE=2EC，设EC=a，则BE=2a，BC=CD=MN=3a． ∵DG=GE，∠DGE=90°，易证△DGN≌△GEM，设EM=x，则GN=EM=x，GM=DN=CM=a+x，∴x+x+a=3a，∴x=a，∴BM=EM．∵GM⊥BE，...

    查看答案和解析>>

    同步练习册答案