
科目:初中数学 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
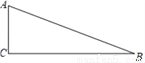
如图,已知△ABC,∠C=90°.请用尺规作一个正方形,使C为正方形的一个顶角,其余三个顶点分别在AB、BC、AC边上.(保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
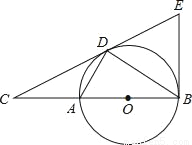
如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:单选题
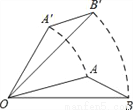
如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是( )
A. 21° B. 45° C. 42° D. 24°
D 【解析】 如图,由题意及旋转变换的性质得:∠BOB′=45°, ∵∠AOB=21°, ∴∠AOB′=45°?21°=24°, 故选D.查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:解答题
有一种螃蟹,从河里捕获后不放养最多只能活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去,假设放养期内蟹的个体重量基本保持不变,现有一经销商,按市场价收购了这种活蟹1000千克放养在塘内,此时市场价为每千克30元,据测算,以后每千克活蟹的市场价每天可上升1元,但是放养一天需各种费用支出400元,且平均每天还有10千克蟹死去,假定死蟹均于当天全部售出,售价都是每千克20元.
(1)设x天后每千克活蟹的市场价为P元,写出P关于x的函数关系式.
(2)如果放养x天后将活蟹一次性出售,并记1000千克蟹的销售额为Q元,写出Q关于X的函数关系式.
(3)该经销商将这批蟹放养多少天后出售,可获最大利润(利润=销售总额-收购成本-费用),最大利润是多少?
(1)p=30+x (2)当x=25时,总利润最大,最大利润为6250元 【解析】(1)由题意知:p=30+x, (2)由题意知 活蟹的销售额为(1000-10x)(30+x)元, 死蟹的销售额为200x元. ∴Q=(1000-10x)(30+x)+200x=-10x2+900x+30000. (3)设总利润为 L=Q-30000-400x=-10x...查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:填空题
在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
< 【解析】试题解析:∵一次函数y=2x+1中k=2>0, ∴y随x的增大而增大, ∵x1<x2, ∴y1<y2.查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:单选题
在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 3 | 3 | 4 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A. 1.70,1.65 B. 1.70,1.70 C. 1.65,1.70 D. 3,3
B 【解析】第8和第9位同学的成绩是1.70,1.70,故中位数是1.70; 数据1.70出现的次数最多,故众数是1.70. 故选B.查看答案和解析>>
科目:初中数学 来源:四川省西昌市航天学校2017-2018学年七年级上册数学期中测试卷(含答案) 题型:解答题
解下列方程: (1)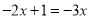 (2)
(2)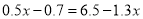
(3)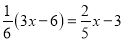 (4)
(4)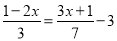
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:解答题
重庆某油脂公司生产销售菜籽油、花生油两种食用植物油.
(1)已知花生的出油率为56%,是菜籽的1.4倍,现有菜籽、花生共100吨,若想得到至少52吨植物油,则其中的菜籽至多有多少吨?
(2)在去年的销售中,菜籽油、花生油的售价分别为20元/升,30元/升,且销量相同,今年由于花生原材料价格上涨,花生油的售价比去年提高了a%,菜籽油的售价不变,总销量比去年降低a%,且菜籽油、花生油的销量均占今年总销量的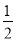 ,这样,预计今年的销售总额比去年下降
,这样,预计今年的销售总额比去年下降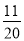 a%,求a的值.
a%,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com