练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

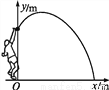
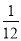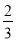    如图,一男生推铅球时,铅球行进高度y(m)与水平距离x(m)之间满足函数关系式y=-x2+x+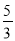,则铅球推出的距离为_____.

    10m 【解析】试题解析：令y=0,得-x2+x+=0. 解得x1=-2(舍去),x2=10, 故铅球推出的距离是10 m. 故答案为：10 m.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期中测评 题型：单选题

    在如图所示的方格纸中,△ABC经过变换得到△DEF,正确的变换是( 　)

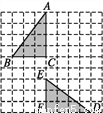
    A. 把△ABC绕点C逆时针方向旋转90°,再向下平移2格

    B. 把△ABC绕点C顺时针方向旋转90°,再向下平移5格

    C. 把△ABC向下平移4格,再绕点C逆时针方向旋转180°

    D. 把△ABC向下平移5格,再绕点C顺时针方向旋转180°

    B 【解析】试题分析：几何变换只改变图形的位置，不改变图形的形状与大小，观察图象可知，C与F，A与D，B与E分别是对应点，由长度可知AC与DF，EF与BC，AB与DE是对应边，∴先把△ABC绕点C顺时针方向旋转90°，再向下平移5格即可得到△DEF．故选B．

    查看答案和解析>>

    科目：初中数学 来源：重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型：解答题

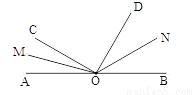
    如图所示，∠AOB是平角，OM、ON分别是∠AOC、∠BOD 的平分线．

    （1）知∠AOC=40°，∠BOD=60°，求∠MON的度数；

    （2）知∠COD=90°，求出∠MON的度数．

    （1）130°；（2）135°． 【解析】试题分析：（1）根据平角即可求得∠COD的度数，再根据角平分线的定义求得∠COM和∠DON的度数，从而求得∠MON的度数； （2）因为OM、ON分别是∠AOC、∠BOD的平分线，故知∠MOC+∠NOD=∠AOC+∠BOD=（∠AOC+∠BOD）即可解答． 试题解析：（1）∵∠AOB是平角，∠AOC=40°，∠BOD=60°， ∴∠C...

    查看答案和解析>>

    科目：初中数学 来源：重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型：单选题

    如图是一个长方体包装盒，则它的平面展开图是（　　）

    A.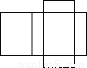

    B.

    C.

    D.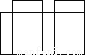

    A 【解析】试题分析：由四棱柱四个侧面和上下两个底面的特征可知，A、可以拼成一个长方体，B、C、D、不符合长方体的展开图的特征，故不是长方体的展开图．故选A．

    查看答案和解析>>

    科目：初中数学 来源：2018春季学北师大版九年级数学下册期中测评试卷 题型：解答题

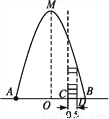
    如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C处(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4 m,AC=3 m,网球飞行最大高度OM=5 m,圆柱形桶的直径为0.5 m,高为0.3 m(网球的体积和圆柱形桶的厚度忽略不计).

    (1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?

    (2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?

    （1）不能；（2）当竖直摆放圆柱形桶8,9,10,11或12个时,网球可以落入桶内. 【解析】【解析】 （1）以点O为原点，AB所在直线为x轴建立直角坐标系（如图）．……（1分） M（0，5），B（2，0），C（1，0），D（，0） 设抛物线的解析式为，抛物线过点M和点B，则， ． 即抛物线解析式为． ……（4分） 当x＝时，y＝；当x＝时，y＝． 即P（1，...

    查看答案和解析>>

    科目：初中数学 来源：2018春季学北师大版九年级数学下册期中测评试卷 题型：填空题

    如图是一张宽为m的矩形台球桌ABCD,一球从点M(点M在长边CD上)出发沿虚线MN射向边BC,然后反弹到边AB上的点P.如果MC=n,∠CMN=α,那么点P与点B的距离为_____. 

    【解析】试题分析：由于P点沿MN经边BC反弹到AB，那么∠PNB＝∠MNC，即∠BPN＝a，可在Rt△MNC中，用a和MC的长表示出NC，进而可求出BN的表达式；进一步可在Rt△PBN中，求出PB的长．

    查看答案和解析>>

    科目：初中数学 来源：2018春季学北师大版九年级数学下册期中测评试卷 题型：单选题

    已知二次函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是(　　)

    A. 当a=1时,函数图象过点(-1,1) B. 当a=-2时,函数图象与x轴没有交点

    C. 若a>0,则当x≥1时,y随x的增大而减小 D. 若a<0,则当x≤1时,y随x的增大而增大

    D 【解析】试题分析：把a=1，x=﹣1代入y=ax2﹣2ax﹣1，于是得到函数图象不经过点（﹣1，1），根据△=8＞0，得到函数图象与x轴有两个交点，根据抛物线的对称轴为直线x=1判断二次函数的增减性． A、∵当a=1，x=﹣1时，y=1+2﹣1=2，∴函数图象不经过点（﹣1，1），故错误； B、当a=﹣2时，∵△=42﹣4×（﹣2）×（﹣1）=8＞0，∴函数图象与x轴有两个交...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（人教版）期末检测题 题型：填空题

    从学校七年级中抽取100名学生，调查学校七年级学生双休日用于数学作业的时间，调查中的总体是　 　　　　　　　　　　　　，个体是　　　　　　　　　　　　　　，样本容量是　　　　。

    七年级学生双休日用于数学作业的时间 七年级每个学生双休日用于数学作业的时间 100 【解析】根据总体，个体，样本容量的概念即可 总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省平凉市崆峒区2017-2018学年度第一学期期末数学试卷及答案 题型：解答题

    某工作甲单独做需15 h完成，乙单独做需12 h完成，若甲先单独做1小时，之后乙再单独做4 h，剩下的工作由甲、乙两人一起做。问：再做几小时可以完成全部工作？

    4 【解析】试题分析：设再做x小时全部完成工作，根据总工作量=甲独做的工作量+乙独做的工作量+甲乙合做的工作量建立等量关系列出方程求出其解就可以了． 试题解析：【解析】 设再做x小时全部完成工作．由题意得： 解得：x=4． 答：再做4小时可以完成全部工作．

    查看答案和解析>>

    同步练习册答案