
绝对值等于7的数是( )
A.7 B.-7 C.±7 D.0和7
C 【解析】 试题分析:绝对值的规律:正数和0的绝对值等于它本身,负数的绝对值等于它的相反数. 绝对值等于7的数是±7,故选C.科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:解答题
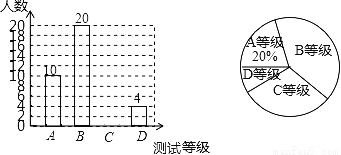
抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
如图,已知AB是半圆O的直径,∠BAC=32º,D是弧AC的中点,那么∠DAC的度数是( )
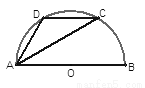
A. 25º B. 29º C. 30º D. 32°
B 【解析】试题分析:连接BC,∵AB是半圆O的直径,∠BAC=32°,∴∠ACB=90°,∠B=90°﹣32°=58°,∴∠D=180°﹣∠B=122°,∵D是的中点,∴∠DAC=∠DCA=÷2=29°,故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:填空题
当x=_____时,式子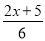 与
与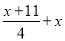 的值互为相反数.
的值互为相反数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:单选题
中国的领水面积约为370000km2,将数370000用科学记数法表示为( )
A. 37×104 B. 3.7×104 C. 0.37×106 D. 3.7×105
D 【解析】试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数,即370000=3.7×105. 故选:D.查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:解答题
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
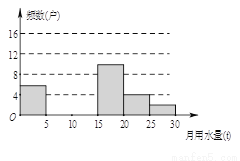
请解答以下问题:
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)填空: 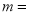 ,
, 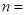 ,并把频数分布直方图补充完整;
,并把频数分布直方图补充完整;
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“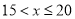 ”的圆心角的度数是 ;
”的圆心角的度数是 ;
(4)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
(1)抽样调查,50 (2)12,0.08 (3)72°(4)640户 【解析】试题分析:(1)由调查了小区部分家庭可知是抽样调查,根据0<x≤5中频数为6,频率为0.12,则调查总户数为6÷0.12=50,则样本容量为50; (2)用样本容量×根据5<x≤10中频率0.12即可得m,用4÷样本容量即可得n,根据m 的值以及16补全统计图即可; (3)用0.2乘以360度即可得;...查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:填空题
无论a取什么实数,动点P(2a,-4a+4)总在直线l上运动,点A的坐标为(-3,0),则线段AP的最小值是______.
; 【解析】∵令a=0,则P(0,4);再令a=1,则P(2,0),由于a不论为何值此点均在直线l上, ∴设此直线的解析式为y=kx+b(k≠0), ∴ ,解得 , ∴此直线的解析式为:y=-2x+4, 易得C(2,0)、D(0,4),所以OC=2,OD=4,AB= , ∵A(-3,0),∴AC=5, 过点A作AB⊥CD于点B,则AB的长即为线段AP的最小...查看答案和解析>>
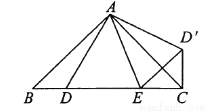
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:解答题
如图,已知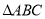 中,
中, 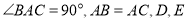 是
是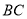 边上的点,将
边上的点,将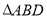 绕点
绕点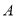 旋转,得到
旋转,得到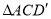 .
.
(1)当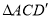 时,求证:
时,求证: 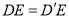 .
.
(2)在(1)的条件下,猜想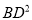 ,
, 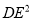 ,
, 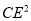 有怎样的数量关系,并说明理由.
有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
在平面直角坐标系中,将抛物线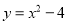 先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )
先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )
A. 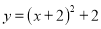 B.
B. 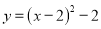 C.
C. 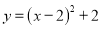 D.
D. 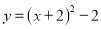
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com