无论a取什么实数.动点P总在直线l上运动.点A的坐标为.则线段AP的最小值是． , [解析]∵令a=0.则P.由于a不论为何值此点均在直线l上. ∴设此直线的解析式为y=kx+b. ∴ .解得 . ∴此直线的解析式为:y=-2x+4. 易得C.所以OC=2.OD=4.AB= . ∵A.∴AC=5. 过点A作AB⊥CD于点B.则AB的长即为线段AP的最小... 题目和参考答案——青夏教育精英家教网—

无论a取什么实数，动点P（2a，-4a+4）总在直线l上运动，点A的坐标为（-3,0），则线段AP的最小值是______．

；【解析】∵令a=0，则P（0，4）；再令a=1，则P（2，0），由于a不论为何值此点均在直线l上， ∴设此直线的解析式为y=kx+b（k≠0）， ∴ ，解得， ∴此直线的解析式为：y=-2x+4，易得C（2，0）、D（0，4），所以OC=2，OD=4，AB= ， ∵A（-3，0），∴AC=5，过点A作AB⊥CD于点B，则AB的长即为线段AP的最小...

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：单选题

如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（　　）

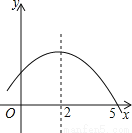
A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5

D 【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0）， ∴函数图象与x轴的另一交点坐标为（-1，0）， ∴ax2+bx+c＜0的解集是x＜-1或x＞5．故选C.

查看答案和解析>>

科目：初中数学 来源：2017-2018学年福建省龙岩市上杭县城区片三校七年级（上）联考数学试卷 题型：解答题

计算：

（1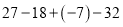）；（2）．

（1）-30；（2）【解析】试题分析：（1）直接计算.(2)按照有理数混合运算法则计算. 试题解析：（1）原式=27+（-18）+（-7）+（-32）= -30. （2）原式= = = =.

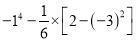查看答案和解析>>

科目：初中数学 来源：2017-2018学年福建省龙岩市上杭县城区片三校七年级（上）联考数学试卷 题型：单选题

绝对值等于7的数是（）

A．7 B．－7 C．±7 D．0和7

C 【解析】试题分析：绝对值的规律：正数和0的绝对值等于它本身，负数的绝对值等于它的相反数. 绝对值等于7的数是±7，故选C.

查看答案和解析>>

科目：初中数学 来源：江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型：解答题

已知一次函数y1＝kx＋b的图像经过点（0，-2），（2，2）.

（1）求一次函数的表达式，并在所给直角坐标系中画出此函数的图像；；

（2）根据图像回答：当x 时，y1=0；

（3）求直线y1＝kx＋b、直线y2＝-2x+4与y轴围成的三角形的面积．

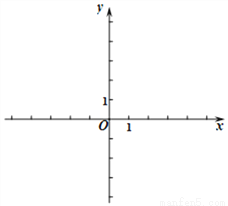
（1）y＝2x-2 （2）x=1 （3）【解析】试题分析：（1）利用待定系数法将坐标代入解析式，解方程组即可得解析式，经过给的两点即可画出函数的图象；（2）观察图象即可得；（3）求出两个函数图象的交点，两函数图象与y轴的交点，然后利用三角形面积公式即可得. 试题解析：（1）由一次函数y1＝kx＋b的图像经过点（0，-2），（2，2），则有，解得：，所以解析式...

查看答案和解析>>

科目：初中数学 来源：江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型：填空题

如果点B (n2－4，－n－3) 在y轴上，那么n=__________．

2/-2；【解析】∵B（n2-4，-n-3）在y轴上， ∴n2-4=0，解得：n=±2，故答案为：±2．

查看答案和解析>>

科目：初中数学 来源：江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型：单选题

下列条件中，不能判断△ABC为直角三角形的是（）

A. a=1.5 b=2 c=2.5 B. a：b：c=5：12：13

C. ∠A＋∠B=∠C D. ∠A：∠B：∠C=3：4：5

D 【解析】A. a2+b2=1.52+22=2.52=c2，所以能判断△ABC是直角三角形，故不符合题意；B. a：b：c=5：12：13，52+122=132，所以能判断△ABC是直角三角形，故不符合题意；C. ∠A＋∠B=∠C ， ∠A＋∠B+∠C =180°，所以∠C=90°，△ABC是直角三角形，故不符合题意； D. ∠A：∠B：∠C=3：4：5，3+4≠5，所以△ABC表示...

查看答案和解析>>

科目：初中数学 来源：吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型：填空题

如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为．

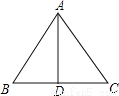
55°．【解析】试题分析：由等腰三角形的三线合一性质可知∠BAC=70°，再由三角形内角和定理和等腰三角形两底角相等的性质即可得出结论．【解析】 AB=AC，D为BC中点， ∴AD是∠BAC的平分线，∠B=∠C， ∵∠BAD=35°， ∴∠BAC=2∠BAD=70°， ∴∠C=（180°﹣70°）=55°．故答案为：55°．

查看答案和解析>>

科目：初中数学 来源：福建省汀东教研片六校2018届九年级10月月考数学试卷 题型：解答题

要设计一幅宽20cm，长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2∶3，如果要使所有彩条所占面积为原矩形图案面积的三分之一，应如何设计每个彩条的宽度？

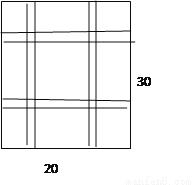
每个横、竖彩条的宽度分别为cm、cm. 【解析】试题分析：设每个横彩条的宽为2xcm，则每个竖彩条的宽为3xcm．求出剩余部分的面积，根据剩余部分的面积是原图案面积的列方程求解即可．试题解析：解:设每个横彩条的宽为2xcm，则每个竖彩条的宽为3xcm． ∴剩余部分的宽为：(20－6x)cm，剩余部分的长为：(30－4x)cm， ∴剩余部分矩形的面积为：(20－6x...

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学