
��֪һ�κ���y=kx��b��ͼ��M(0��2)��N(1��3)���㣮
(1)��k��b��ֵ��
(2)��һ�κ���y=kx��b��ͼ����x�ύ��ΪA(a��0)����a��ֵ��
��1��k��b��ֵ�ֱ���1��2����2��a=��2. �������������������1�����ݴ���ϵ�������һ�κ�������ʽ���ɣ� ��2������ͼ���뺯�������ύ�������ó�a��ֵ�� �������� ��1��������ã� ��ã� ��k��b��ֵ�ֱ���1��2�� ��2����k=1��b=2����y=kx+b�е�y=x+2�� �ߵ�A��a��0���� y=x+2��ͼ���ϣ� ��0=a+2�� ��...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ����˽̰���꼶��ѧ�²��26 ��ͬ����ʱ��ϰ��26.2 ʵ�������뷴������������1��ʱ�� ���ͣ������
������ٹ�·ȫ��658km�������ؾ�����ٹ�·������ʻ������������������ȫ������ʱ�� t��h������ʻ��ƽ���ٶ� v��km/h��֮��ĺ�����ϵʽΪ ��
t= �����������������������ã� ������ʻ��ȫ�������ʱ��t����ʻ��ƽ���ٶ�v֮��ĺ�����ϵʽ��t=�� �ʱ����Ϊ��t=���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧ ������ ��ʽ�ֽ� ��Ԫ���� ���ͣ���ѡ��
�ֽ���ʽ��4x2y+2xy2��xy�Ľ���ǣ� ��
A����4��x2+2xy2��xy�� B����xy����4x+2y��1��
C����xy��4x��2y+1�� D����xy��4x��2y��
C �������� �����������4x2y+2xy2��xy��ȡ����ʽ-xy�ã�ԭʽ=-xy(4x-2y+1)����ѡC�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��²�16.1���θ�ʽ ͬ����ϰ ���ͣ���ѡ��
��x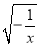 ������������Ƶ������ڣ�����ǣ�������
������������Ƶ������ڣ�����ǣ�������
A. 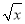 B.
B. 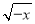 C. -
C. -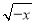 D. -
D. -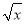
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��4�� һ�κ��� ��Ԫ���Ծ� ���ͣ������
�ס��������ֱ��A��B����ͬʱ����������У����Ը��Ե��ٶ�������ʻ���׳�;��C��ʱ��ϢһСʱ��Ȼ��ԭ�ٶȼ���ǰ������B�أ��ҳ���B��ֱ�ӵ���A�أ���ͼ�Ǽס���������B�صľ���y��ǧ�ף���׳�����ʱ��x��Сʱ���ĺ���ͼ��
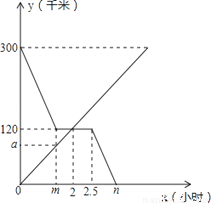
��1��ֱ��д��a��m��n��ֵ��
��2������׳���B�صľ���y��ǧ�ף���׳�����ʱ��x��Сʱ���ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ����
��3�����������120ǧ��ʱ���ҳ���ʻ�˶ʱ�䣿
��1��a=90��m=1.5��n=3.5�� ��2��y��x�Ĺ�ϵʽΪ ��3���ҳ���ʻ��1Сʱ��3Сʱ �������������������1���׳�;��C��ʱ��ϢһСʱ����2.5��m=1����m=1.5�� ���ҳ����ٶ�Ϊ�� ���������a=90�� �׳����ٶ�Ϊ�� �����n=3.5�� ��a=90��m=1.5��n=3.5�� ��2������Ϣǰ����Ϣʱ����Ϣ�������Σ����ô���ϵ������һ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��4�� һ�κ��� ��Ԫ���Ծ� ���ͣ������
��֪����x�ķ���ax��5=7�Ľ�Ϊx=1����һ�κ���y=ax��12��x�ύ�������Ϊ________��
(1��0) �������������������x=1�ǹ���x�ķ���ax-5=7�Ľ⣬ ��a-5=7�� ���a=12�� ��һ�κ���y=ax-12������Ϊy=12x-12. ��y=0���õ���12x-12=0�� ���x=1�� ��һ�κ���ͼ����x��Ľ��������ǣ�1��0��. �ʴ�Ϊ����1��0��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��4�� һ�κ��� ��Ԫ���Ծ� ���ͣ���ѡ��
ֱ��y=��2x��b��x��Ľ���������(2��0)�������x�ķ���2x��b=0�Ľ���(����)
A. x=2 B. x=4 C. x=8 D. x=10
A ���������������������ֱ��y=kx+b��ͼ����x�ύ��ĺ�������Ƿ���kx+b=0�Ľ⼴�ɵñ���𰸣��ʴ�ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��16�� ���θ�ʽ ��Ԫ���� ���ͣ������
��֪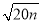 ����������������������С������nΪ________
����������������������С������nΪ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭����������������ѧ2017-2018ѧ����꼶��ѧ��������ѧ ���ͣ������
���⡰���������ε������ϵĸ�����ȡ� ���������ǣ�_______________________��
�����ϸ�����ȵ��������ǵ��������� ���������������� ���⡰���������������ϵĸ���ȡ����������ǣ������ϸ�����ȵ��������ǵ��������Σ� �ʴ�Ϊ�������ϸ�����ȵ��������ǵ��������Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com