
表格描述的是y与x之间的函数关系:
x | … | -2 | 0 | 2 | 4 | … |
y=kx+b | … | 3 | -1 | m | n | … |
则m与n的大小关系是____________.
m>n 【解析】∵当x=?2,y=3,x=0,y=?1, ∴y随着x的增大而减小, ∵2<4, ∴m>n. 故答案为:m>n.科目:初中数学 来源:山东省德州地区2017-2018学年度七年级第一学期期末检测数学试卷 题型:单选题
关于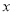 的方程
的方程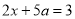 的解与方程
的解与方程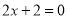 的解相同,则
的解相同,则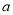 的值是( )
的值是( )
A. 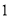 B.
B. 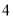 C.
C. 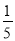 D.
D. 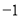
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十六章达标检测卷 题型:解答题
(a2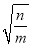 -
-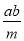
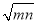 +
+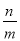
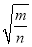 )÷a2b2
)÷a2b2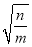 ;
;
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十六章达标检测卷 题型:填空题
当x__________ 时,式子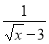 有意义
有意义
查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:解答题
在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
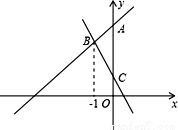
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.
①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于 ;
(2)直线y=kx+4(k≠0)与x轴交于点E(x 0 ,0),若﹣2<x 0 <﹣1,求k的取值范围.
(1)①B(-1,3);k=1;②、1.5;(2)2<k<4. 【解析】试题分析:(1)将点B的横坐标代入y=-2x+1得出点B的纵坐标,将点B的坐标代入y=kx+4求出k的值;根据解析式求出A、C的坐标,然后进行计算;(2)用k的代数式表示点E的横坐标,然后根据不等式求出k的取值. 试题解析:(1)①将x=-1代入y=-2x+1得:y=-2×(-1)+1=3,∴点B的坐标为(-1,3...查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:单选题
为了节省空间,家里的饭碗一般是摞起来存放的.如果6只饭碗摞起来的高度为15 cm,9只饭碗摞起来的高度为20 cm,那么11只饭碗摞起来的高度更接近( )
A. 21cm B. 22cm C. 23cm D. 24cm
C 【解析】试题分析:设碗的个数为xcm,碗的高度为ycm,可得碗的高度和碗的个数的关系式为y=kx+b,根据6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,列方程组求解,然后求出11只饭碗摞起来的高度. 试题解析:设碗身的高度为xcm,碗底的高度为ycm, 由题意得, , 解得: 则11只饭碗摞起来的高度为: ×11+5=23(cm). ...查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:单选题
下列函数是一次函数的是( )
A. -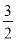 x2+y=0 B. y=4x2-1 C. y=
x2+y=0 B. y=4x2-1 C. y=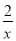 D. y=3x
D. y=3x
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型:单选题
点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=3 cm,则点P到直线l的距离( )
A. 等于4 cm B. 等于5 cm C. 小于3 cm D. 不大于3 cm
D 【解析】试题解析:∵直线外一点与直线上各点连接的所有线段中,垂线段最短, ∴点P到直线a的距离≤PC, 即点P到直线a的距离不大于3cm. 故选D.查看答案和解析>>
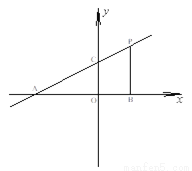
科目:初中数学 来源:2018人教版八年级数学下册练习:期末达标检测卷 题型:解答题
若直线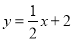 分别交
分别交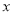 轴、
轴、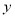 轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥
轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥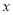 轴,B为垂足,且S⊿ABC= 6.
轴,B为垂足,且S⊿ABC= 6.
(1)求点B和P的坐标;
(2)过点B画出直线BQ∥AP,交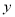 轴于点Q,并直接写出点Q的坐标.
轴于点Q,并直接写出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com